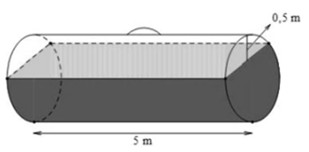
(4,0 điểm)

Vườn nhà bạn Minh có trồng loại dưa hấu hình vuông. Trong hình dưới là quả dưa hấu hình vuông có cạnh dài \(18\)cm.

a) Tính thể tích của quả dưa hấu hình vuông.

b) Minh muốn cắt quả dưa hấu thành những hình vuông nhỏ có cạnh \(5\)cm để bày ra đĩa và

dự định mỗi đĩa bày \(12\) miếng dưa. Hỏi Minh có thể bày được mấy đĩa? ( Làm tròn đến

hàng đơn vị).

 

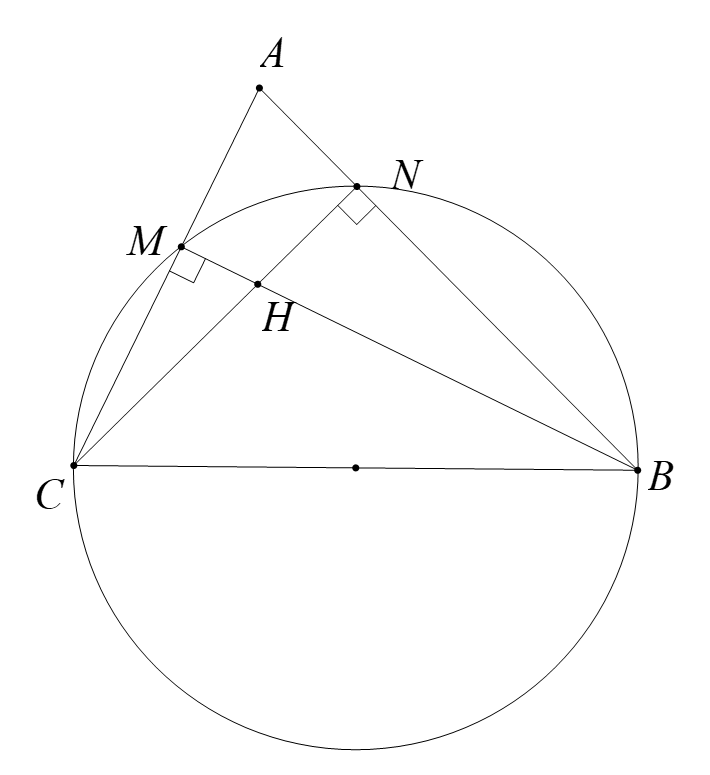
a/ Chứng minh tứ giác \[AMHN\] nội tiếp

Các đường cao \[BM,\;\,\,CN\] cắt nhau tại\[H\]nên ta có \(\Delta ANH,\,\,\Delta AMH\) vuông tại \[N,\,\,M\]

Xét \(\Delta ANH\) có \[\widehat {ANH} = 90^\circ \] nên ba điểm \(A,\;N,\;H\) nằm trên đường tròn đường kính \(AH\)

Xét \(\Delta AMH\) có \[\widehat {AMH} = 90^\circ \] nên ba điểm \(A,\;M,\;H\) nằm trên đường tròn đường kính \(AH\)

Khi đó bốn điểm \(A,\,\,M,\,\,H,\,\,N\) nằm trên đường tròn đường kính \(AH\)

Vậy tứ giác \[AMHN\]  nội tiếp đường tròn đường kính\[AH\].

 b/ Gọi \[D\] là giao điểm của \[AH\]và\[BC\]. Chứng minh \[DA\] phân giác của \[\widehat {MDN}\]

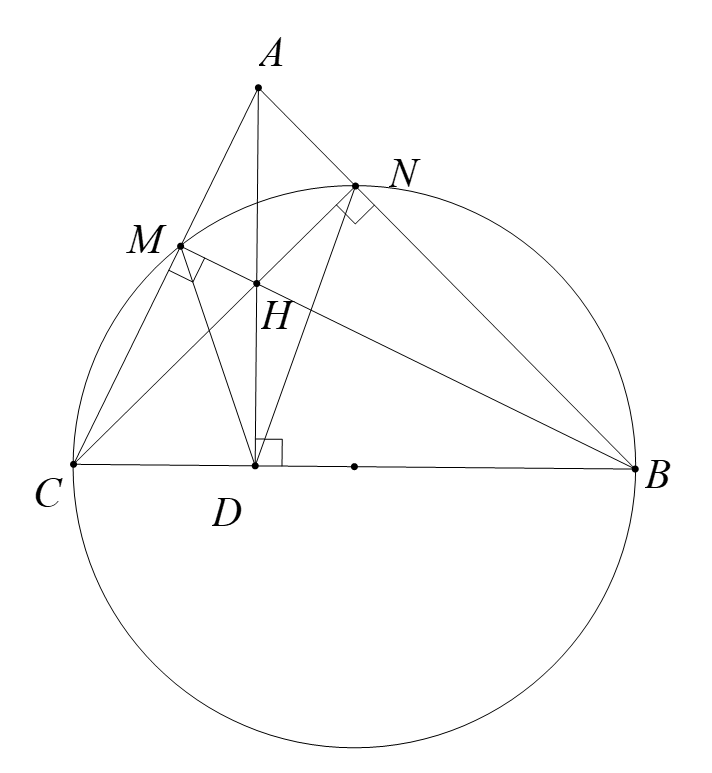
Có \[\widehat {HMC} = \widehat {HDC} = 90^\circ \]

Xét \(\Delta HMC\) có \[\widehat {HMC} = 90^\circ \] nên ba điểm \(C,\,\,M,\,\,H\) nằm trên đường tròn đường kính \(CH\)

Xét  \(\Delta CDH\)có \[\widehat {HDC} = 90^\circ \] nên ba điểm \(C,\,\,D,\,\,H\) nằm trên đường tròn đường kính \(CH\)

Khi đó bốn điểm \(D,\,\,C,\,\,M,\,\,H\) nằm trên đường tròn đường kính \(CH\)

Suy ra tứ giác \[HDCM\] nội tiếp

Suy ra \[\widehat {HDM} = \widehat {HCM}\] (2 góc nội tiếp cùng chắn cung\[HM\])

Có \[\widehat {HDB} = \widehat {HNB} = 90^\circ {\rm{ }}\]

Xét \(\Delta HDB\) có \[\widehat {HDB} = 90^\circ \] nên ba điểm \(B,\,\,D,\,\,H\) nằm trên đường tròn đường kính \(BH\)

Xét \(\Delta HNB\) có \[\widehat {HNB} = 90^\circ \] nên ba điểm \(B,\,\,N,\,\,H\) nằm trên đường tròn đường kính \(BH\)

Khi đó bốn điểm \(D,\,\,B,\,\,N,\,\,H\) nằm trên đường tròn đường kính \(BH\)

Suy ra tứ giác \[HDBN\]  nội tiếp

\[\widehat {NDH} = \widehat {NBH}\] (2 góc nội tiếp cùng chắn cung\[HN\])

Mà \[\widehat {HCM} = \widehat {NBH}\](cùng phụ với\[\widehat {BAC}\])

Suy ra \[\widehat {HDM} = \widehat {HDN}\] Suy ra \[AD\] là phân giác của góc \[\widehat {MDN}\](đpcm).

c/Đường thẳng qua \[D\] và song song với \[MN\,\] cắt \[AB,\,\,CN\] lần lượt tại \[I,\,\,J\]. Chứng minh \[D\] là

trung điểm \[IJ\].

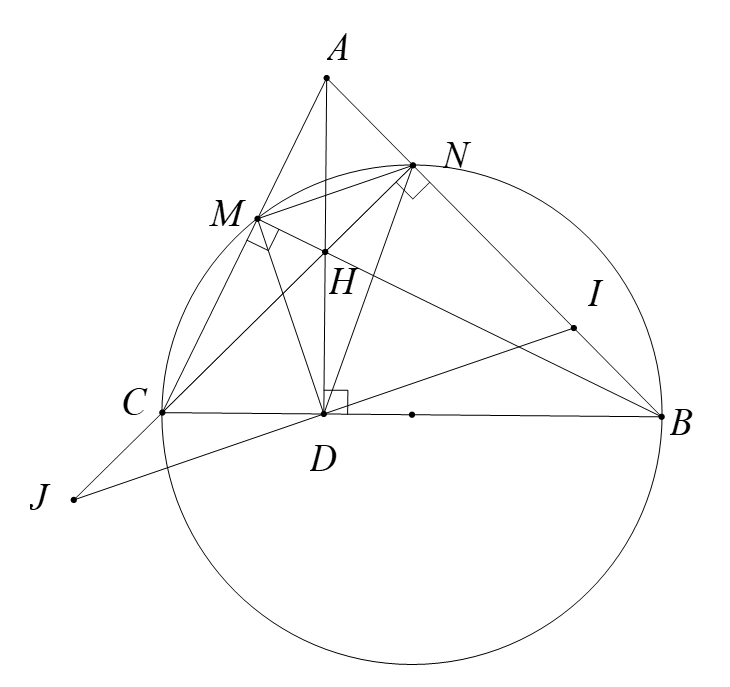
Có \[\widehat {BMC} = \widehat {CNB} = 90^\circ {\rm{ }}\]

Xét \(\Delta MCB\) có \[\widehat {BMC} = 90^\circ \] nên ba điểm \(B,\,\,M,\,\,C\) nằm trên đường tròn đường kính \(BC\)

Xét \(\Delta BNC\) có \[\widehat {BNC} = 90^\circ \] nên ba điểm \(B,\,\,N,\,\,C\) nằm trên đường tròn đường kính \(BC\)

Khi đó bốn điểm \(C,\,\,B,\,\,N,\,\,M\) nằm trên đường tròn đường kính \(BC\)

Suy ra tứ giác \[BCMN\] nội tiếp

Suy ra \[\widehat {HNM} = \widehat {HBD}\] (hai góc nội tiếp cùng chắn một cung \(CM\))

Tứ giác \(HDBN\) nội tiếp nên \(\widehat {HBD} = \widehat {HND}\)( hai góc nội tiếp cùng chắn một cung \(HD\))

Suy ra \[\widehat {HNM} = \widehat {HND}\]

Ta có \(IJ\,{\rm{//}}\,MN\,\,\left( {gt} \right)\) Suy ra \(\widehat {HNM} = \widehat {HJI} = \widehat {HJD}\) (Hai góc so le trong bằng nhau)

Suy ra \[\widehat {HND} = \widehat {HJD}\]

Nên tam giác \[DNJ\] cân tại \[D\] (tam giác có 2 góc ở đáy bằng nhau)

Suy ra \[DN = DJ\] (tính chất tam giác cân) (1)

Vì \(\widehat {HND} = \widehat {HJD}\) (chứng minh trên)

Mà \(\widehat {HND} + \widehat {DNI} = \widehat {HNI} = 90^\circ \) và \(\widehat {HJD} + \widehat {NID} = 90^\circ \)( do \(\Delta JNI\) vuông tại \[N\])

Suy ra \[\widehat {DNI} = \widehat {NID}\]

Tam giác \(\Delta NID\) cân tại \[D\] (tam giác có 2 góc ờ đáy bằng nhau)

Suy ra \[DN = DI\] (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra \(DI = DJ = DN\)

Vậy \[D\] là trung điểm \[IJ\]