(4,0 điểm)
Một hộp bóng hình trụ chứa vừa khít \(3\)quả bóng tennis có đường kính \(6,5\,cm\) như hình.
a) Tính diện tích bề mặt và thể tích của mỗi quả bóng
b) Tính diện tích xung quanh và thể tích của hộp bóng.

a) Tính diện tích bề mặt và thể tích của mỗi quả bóng
b) Tính diện tích xung quanh và thể tích của hộp bóng.

Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 39 !!
Quảng cáo
Trả lời:
Bán kính quả bóng hình cầu là : \(r = 6,5:2\) \( = 3,25cm\)
Diện tích bề mặt mỗi quả bóng là : \({S_{mc}} = 4\pi {r^2}\) \( = 4.\pi {,3,25^2}\) \( = 42,25\pi \,\left( {c{m^2}} \right)\)
Thể tích của mỗi quả bóng hình cầu là: \(V = \frac{4}{3}\pi {r^3}\) \( = \frac{4}{3}.\pi {.3,25^3}\) \( = \frac{{13,73125\pi }}{3}\,\left( {c{m^3}} \right)\)
b) Tính diện tích xung quanh và thể tích của hộp bóng.
Bán kính hộp bóng hình trụ chính là bán kính của quả bóng hình cầu là: \(r = 6,5:2 = 3,25cm\)
Chiều cao của hộp bóng hình trụ là: \(h = 3.6,5 = 19,5\left( {cm} \right)\)
Diện tích xung quanh hộp bóng hình trụ là : \({S_{xq}} = 2\pi Rh\) \( = 2.\pi .3,25.19.5\) \( = 123,5\pi \,\left( {c{m^2}} \right)\)
Thể tích của hộp bóng hình trụ là: \[V = \pi {r^2}h\] \[ = \pi {.3,25^2}.19,5\] \[ = 205,96875\pi \,\left( {c{m^3}} \right)\]
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn \(\left( O \right)\), từ điểm \(A\)ở ngoài đường tròn vẽ hai tiếp tuyến \(AB\)và\(AC\)(\(B,\,\,C\)là các tiếp điểm), \(OA\)cắt\(BC\)tại E.
a) Chứng minh tứ giác \(ABOC\) nội tiếp.
b) Chứng minh \(BC\) vuông góc với \(OA\) và \(BA.BE = AE.BO\).
c) Gọi \(I\)thuộc đoạn thẳng \(BE\), đường thẳng qua\(I\)và vuông góc \(OI\)cắt các tia \(AB,\,\,AC\)theo thứ tự tại \(D\)và \(F\). Chứng minh \(F\) là trung điểm của\(AC\).
a) Chứng minh tứ giác \(ABOC\) nội tiếp.
Xét \(\left( O \right)\)có:
\(AB\)là tiếp tuyến tại \(B\) (GT) nên \[AB \bot OB \Rightarrow \widehat {ABO} = 90^\circ \]
\[ \Rightarrow \Delta ABO\]vuông tại \(B\) nên điểm \[B\] thuộc đường tròn đường kính \[AO\] (1)
Mặt khác: \(AC\)là tiếp tuyến tại \(C\) (GT) nên \[AC \bot OC \Rightarrow \widehat {ACO} = 90^\circ \]
\[ \Rightarrow \Delta ACO\]vuông tại \[C\]nên điểm \[C\] thuộc đường tròn đường kính \[AO\] (2)
Từ (1) và (2) sy ra: 4 điểm \(A,B,O,C\) cùng thuộc đường tròn đường kính \[AO\]
Do đó, tứ giác \(ABOC\) nội tiếp đường tròn đường kính \[AO\]
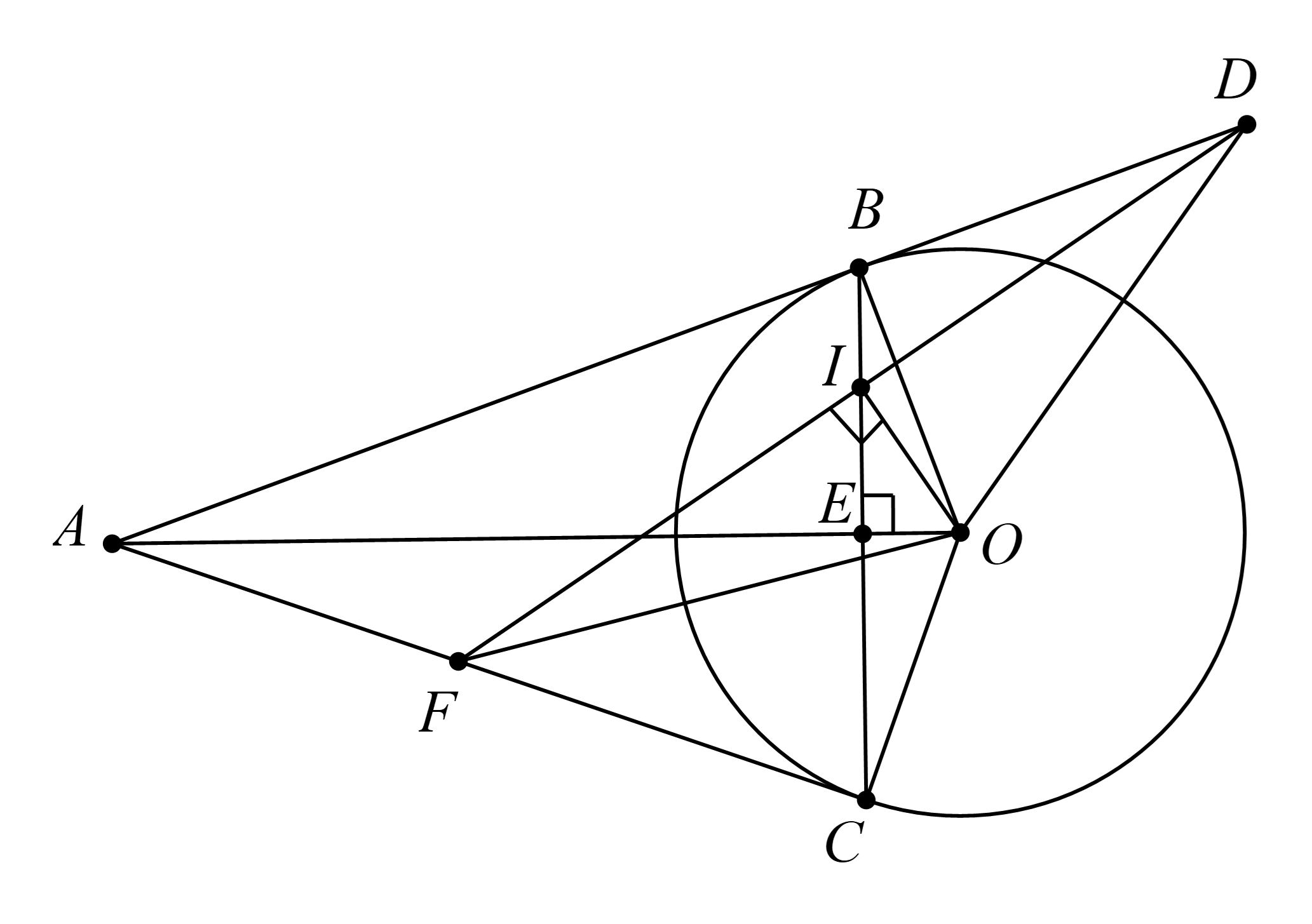
b) Chứng minh \(BC\) vuông góc với \(OA\) và \(BA.BE = AE.BO\).
* Chứng minh \(BC\) vuông góc với \(OA\)
Xét \(\left( O \right)\)có: \(AB\)và\(AC\) là hai tiếp tuyến cắt nhau ở \(A\) (GT)
\( \Rightarrow AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
Mà \(OB = OC\) (\(B,\,\,C\) thuộc đường tròn\(\left( O \right)\))
\( \Rightarrow OA\) là đường trung trực của \(BC\) nên \(BC \bot OA\)
* Chứng minh \(BA.BE = AE.BO\)
Xét \(\Delta ABO\) và \(\Delta AEB\) có:
\(\widehat {ABO} = \widehat {AEB} = 90^\circ \,\,(cmt)\)
\(\widehat {BAO}\): góc chung
Suy ra: \(\Delta ABO\) ~ \(\Delta AEB\) (g.g)
\( \Rightarrow \frac{{AB}}{{AE}} = \frac{{BO}}{{EB}} \Rightarrow AB.EB = AE.BO\)
c) Gọi \(I\)là điểm thộc đoạn thẳng \(BE\), đường thẳng qua\(I\)và vuông góc \(OI\)cắt các tia \(AB,\,\,AC\)theo thứ tự tại \(D\)và \(F\). Chứng minh \(F\) là trung điểm của\(AC\).
Vì \[AB \bot OB \Rightarrow \widehat {DBO} = 90^\circ \]
\[ \Rightarrow \Delta DBO\]vuông tại \(B\) nên điểm \[B\] thuộc đường tròn đường kính \[DO\] (1)
Vì \[OI \bot DF \Rightarrow \widehat {DIO} = 90^\circ \]
\[ \Rightarrow \Delta DIO\]vuông tại \(I\) nên điểm \[I\] thuộc đường tròn đường kính \[DO\] (2)
Từ (1) và (2) sy ra: 4 điểm \(D,B,I,O\) cùng thuộc đường tròn đường kính \[DO\]
Do đó, tứ giác \(DBIO\) nội tiếp đường tròn đường kính \[DO\]
\[ \Rightarrow \widehat {IDO} = \widehat {IBO}\] ( 2 góc nội tiếp cùng chắn cung \[IO\])
CMTT ta có: \[\widehat {IFO} = \widehat {ICO}\]
Mặt khác: \[OB = OC \Rightarrow \Delta OBC\]cân ở \[O \Rightarrow \widehat {OBC} = \widehat {OCB}\] hay \[\widehat {IBO} = \widehat {ICO}\]
Do đó: \[\widehat {IDO} = \widehat {IFO} \Rightarrow \Delta ODF\] cân ở \[O\] mà \[OI \bot DF\] (GT)
\[ \Rightarrow I\] là trung điểm của \[DF\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số tấm kính giọt bắn mỗi lớp \(9A,\;9B\)làm được trong đợt 1 lần lượt là: \(x,\;y\) (tấm) (\(0 < x,y < 1500)\)
Vì trong đợt 1 cả hai lớp \(9A,\;9B\) đã làm được \(1500\)chiếc tấm kính chắn giọt bắn nên ta có phương trình:
\(x + y = 1500\) (1)
Số tấm kính giọt bắn lớp \(9A\)làm được trong đợt 2 là: \(x + 70\% .x = 1,7x\) (tấm)
Số tấm kính giọt bắn lớp \(9B\)làm được trong đợt 2 là: \(y + 68\% .y = 1,68y\) (tấm)
Vì trong đợt 2 cả hai lớp \(9A,\;9B\) đã làm được \(2358\)chiếc tấm kính chắn giọt bắn nên ta có phương trình:
\(1,7x + 1,68y = 2358\) (2)
Từ (1) và (2) ta có hệ phương trình:\(\left\{ \begin{array}{l}x + y = 1500\quad \quad \quad \quad \quad \left( 1 \right)\\1,7x + 1,68y = 2358\quad \quad \left( 2 \right)\end{array} \right.\)
Giải hệ phương trình ta được: \(x = 960\;\left( {TM} \right);\;y = 540\;\left( {TM} \right)\)
Vậy số tấm kính giọt bắn mỗi lớp \(9A,\;9B\)làm được trong đợt 1 lần lượt là: \(960;\;540\) (tấm)
Lời giải
Gọi chiều rộng là \(x\left( {cm} \right)\left( {0 < x < 12} \right)\)
Chiều dài là \(12 - x\left( {cm} \right)\)
Chiều cao là \(24 - x\left( {cm} \right)\)
Ta có thể tích chiếc hộp là: \(V = x\left( {12 - x} \right)\left( {24 - x} \right)\left( {c{m^3}} \right)\)
Bất đẳng thức Cauchy 3 số không âm \(a,b,c\)ta có: \(a + b + c \ge 3\sqrt[3]{{abc}}\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = c\)
Thật vậy, đặt \(x = \sqrt[3]{a},y = \sqrt[3]{b},z = \sqrt[3]{c}\)\( \Rightarrow x,y,z \ge 0 \Rightarrow x + y + z \ge 0\)
Ta phái chứng minh:
\({x^3} + {y^3} + {z^3} \ge 3xyz\)
\({\left( {x + y} \right)^3} - 3xy\left( {x + y} \right) + {z^3} - 3xyz \ge 0\)
\(\left( {x + y + z} \right)\left[ {{{\left( {x + y} \right)}^2} - \left( {x + y} \right)z + {z^2}} \right] - 3xy\left( {x + y + z} \right) \ge 0\)
\(\left( {x + y + z} \right)\left[ {{x^2} + {y^2} + {z^2} + 2xy - xz - yz} \right] - 3xy\left( {x + y + z} \right) \ge 0\)
\(\left( {x + y + z} \right)\left[ {{x^2} + {y^2} + {z^2} - xy - xz - yz} \right] \ge 0\)
\({x^2} + {y^2} + {z^2} - xy - xz - yz \ge 0\) (vì \(x + y + z \ge 0\))
\({\left( {x - y} \right)^2} + {\left( {y - z} \right)^2} + {\left( {z - x} \right)^2} \ge 0\)\(\)(luôn đúng)
Dấu “=” xảy ra khi \(x = y = z\) hay \(a = b = c\)
Áp dụng bất đẳng thức Cauchy cho 3 số không âm ta có:
\(V = x\left( {12 - x} \right)\left( {24 - x} \right)\left( {c{m^3}} \right)\)
\(\frac{1}{{\left( {\sqrt 3 - 1} \right)\left( {2 - \sqrt 3 } \right)}}.x.\left( {\sqrt 3 - 1} \right)\left( {2 - \sqrt 3 } \right)\left( {12 - x} \right)\left( {24 - x} \right)\)
\( \le \frac{1}{{\left( {\sqrt 3 - 1} \right)\left( {2 - \sqrt 3 } \right)}}.{\left[ {\frac{{x + \left( {\sqrt 3 - 1} \right)\left( {12 - x} \right) + \left( {2 - \sqrt 3 } \right)\left( {24 - x} \right)}}{3}} \right]^3}\)
\( = \frac{1}{{\left( {\sqrt 3 - 1} \right)\left( {2 - \sqrt 3 } \right)}}.{\left[ {\frac{{x + 12\sqrt 3 - \sqrt 3 x - 12 + x + 48 - 2x - 24\sqrt 3 + \sqrt 3 x}}{3}} \right]^3}\)
\( = \frac{1}{{\left( {\sqrt 3 - 1} \right)\left( {2 - \sqrt 3 } \right)}}.{\left[ {\frac{{36 - 12\sqrt 3 }}{3}} \right]^3} = 384\sqrt 3 \)
Dấu “=” xảy ra khi và chỉ khi: \(x = \left( {\sqrt 3 - 1} \right)\left( {12 - x} \right)\)\( = \left( {2 - \sqrt 3 } \right)\left( {24 - x} \right)\)\( \Leftrightarrow x = 12 - 4\sqrt 3 \)
Vậy \({V_{\max }} = 384\sqrt 3 \)\( \Leftrightarrow x = 12 - 4\sqrt 3 \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.