(2,5 điểm)
Cách đây hai năm, bác Chín gửi một số tiền vào ngân hàng với lãi suất \(6\% \) một năm. Bây giờ số tiền bác Chính có được cả gốc lẫn lãi là \(33,708\) triệu đồng. Hỏi ban đầu bác Chín gửi vào bao nhiêu tiền?
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 43 !!
Quảng cáo
Trả lời:
Số tiền cả gốc lẫn lãi sau một năm là: \(x + 0,06x = 1,06x\) (triệu đồng)
Số tiền cả gốc và lãi sau năm thứ hai là: \(1,06x.\left( {1 + 6\% } \right) = 1,1236x\) (triệu đồng)
Vì sau hai năm, bác Chín nhận được \(33,9\) triệu đồng cả gốc và lãi, nên ta có phương trình: \(1,1236x = 33,708\)
\(x = 33,708:1,1236 = 30\) (thỏa mãn)
Vậy số tiền ban đầu bác Chín gửi vào là \(30\) triệu đồng.
Câu hỏi cùng đoạn
Câu 2:
Hai đội công nhân dệt may cần sản xuất một số lượng khẩu trang theo đơn đặt hàng. Nếu làm chung thì sau giờ họ sẽ làm xong. Nhưng hai đội mới làm chung được giờ thì đội nghỉ , đội tiếp tục làm trong giờ nữa mới xong. Hỏi mỗi đội nếu làm một mình thì phải bao lâu mới xong công việc ?
Gọi thời gian đội 1 hoàn thành công việc một mình là \(x\) (giờ, \(x > 4\))
Gọi thời gian đội 2 hoàn thành công việc một mình là \(y\) (giờ, \(y > 4\))
Trong một giờ, đội 1 làm được số phần công việc là: \(\frac{1}{x}\) (công việc); đội 2 làm được số phần công việc là: \(\frac{1}{y}\) (công việc).
Trong một giờ, cả hai đội là được số phần công việc là: \(\frac{1}{x} + \frac{1}{y}\). Trong bốn giờ, cả hai đội làm được số phần công việc là: \(4\left( {\frac{1}{x} + \frac{1}{y}} \right)\).
Khi đó cả hai đội làm xong việc nên ta có phương trình là: \(4\left( {\frac{1}{x} + \frac{1}{y}} \right) = 1\) (1)
Trong ba giờ, cả hai đội làm được số phần công việc là: \(3.\left( {\frac{1}{x} + \frac{1}{y}} \right)\) (công việc);
Trong ba giờ, đội 2 làm được số phần công việc là: \(3.\frac{1}{y}\) (công việc).
Khi đó công việc mới xong, nên ta có phương trình: \(3.\left( {\frac{1}{x} + \frac{1}{y}} \right) + 3.\frac{1}{y} = 1\) hay \(3.\frac{1}{x} + 6.\frac{1}{y} = 1\) (2)
Từ (1) và (2), ta có hệ phương trình: \(\left\{ \begin{array}{l}4\left( {\frac{1}{x} + \frac{1}{y}} \right) = 1\\3.\frac{1}{x} + 6.\frac{1}{y} = 1\end{array} \right.\)
Giải hệ phương trình, ta có: \(\left\{ \begin{array}{l}x = 6\\y = 12\end{array} \right.\) (thỏa mãn)
Vậy đội 1 làm một mình trong \(6\) giờ xong, đội 2 làm một mình trong \(12\) giờ xong công việc
Câu 3:
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình: \(3{x^2} + 5x - 6 = 0\). Không giải phương trình, tính các giá trị của các biểu thức \({\rm{D = }}\frac{{{x_1}}}{{{x_2} + 2}} + \frac{{{x_2}}}{{{x_1} + 2}}\).
Phương trình có tích \(ac = 3{\rm{ }}{\rm{. }}\left( { - 6} \right) = - 18 < 0\) nên có nghiệm phân biệt \({x_1}\), \({x_2}\). Theo định lý Viète, ta có \({x_1} + {x_2} = \frac{{ - 5}}{3}\) và \({x_1}{x_2} = - 2\).
\({x_1}\),\({x_2} \ne - 2\)
\({\rm{D = }}\frac{{{x_1}}}{{{x_2} + 2}} + \frac{{{x_2}}}{{{x_1} + 2}} = \frac{{{x_1}\left( {{x_1} + 2} \right) + {x_2}\left( {{x_2} + 2} \right)}}{{\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right)}}\)
\(D = \frac{{\left( {x_1^2 + x_2^2} \right) + 2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\)
\(D = \frac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\)
\(D = \frac{{{{\left( {\frac{{ - 5}}{3}} \right)}^2} - 2{\rm{ }}{\rm{. }}\left( { - 2} \right) + 2{\rm{ }} \cdot {\rm{ }}\left( {\frac{{ - 5}}{3}} \right)}}{{\left( { - 2} \right) + 2{\rm{ }} \cdot {\rm{ }}\left( {\frac{{ - 5}}{3}} \right) + 4}} = \frac{{ - 31}}{{12}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Trong mẫu số liệu trên, số liệu có giá trị nhỏ nhất là \[41\], số liệu có giá trị lớn nhất là \[59\]. Vì thế, ta có thể chọn nửa khoảng \[[40;\,\,60)\] sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng \[[40;\,\,60)\]. Vì độ dài của nửa khoảng \[[40;\,\,60)\] bằng \[60 - 40 = 20\] nên ta có thể phân chia nửa khoảng đó thành bốn nửa khoảng có độ dài bằng nhau là: \[[40;\,\,45)\], \[[45;\,\,50)\], \[\,[50;\,\,55)\]\[\,[55 & ;\,\,60)\].
Vậy ta có thể ghép mẫu số liệu đã cho theo bốn nhóm ứng với bốn nửa khoảng đó.
b) Tốc độ của xe đi từ \[40\] \[{\rm{km/h}}\] đến dưới \[45\] \[{\rm{km/h}}\] là \[7\] xe;
Tốc độ của xe đi từ \[45\] \[{\rm{km/h}}\] đến dưới \[50\] \[{\rm{km/h}}\] là \[7\] xe;
Tốc độ của xe đi từ \[50\] \[{\rm{km/h}}\] đến dưới \[55\] \[{\rm{km/h}}\] là \[5\] xe;
Tốc độ của xe đi từ \[55\] \[{\rm{km/h}}\] đến dưới \[60\] \[{\rm{km/h}}\] là \[6\] xe.
Do đó ta có bảng tần số ghép nhóm
|
Tốc độ \[\left( {{\rm{km/h}}} \right)\] |
\[\left[ {40;{\rm{ }}45} \right)\] |
\[\left[ {45;{\rm{ 50}}} \right)\] |
\[\left[ {50;{\rm{ 55}}} \right)\] |
\[\left[ {55;{\rm{ 60}}} \right)\] |
|
Tần số |
\[7\] |
\[7\] |
\[5\] |
\[6\] |
Lời giải
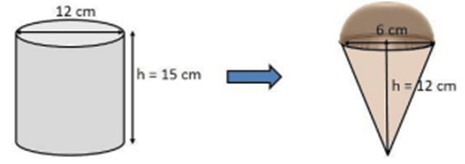
a) Thể tích kem trong hộp hình trụ là: \[{V_T} = \pi R_T^2.{h_T}\]\[ = \pi {\left( {\frac{{12}}{2}} \right)^2}.15\]\[ = 540\pi \,\,(c{m^3})\]
b) Thể tích kem trong hộp hình nón có hình bán cầu trên đỉnh là \[{V_{kem}} = \frac{1}{3}\pi R_N^2.{h_N} + \frac{1}{2}.\frac{4}{3}\pi R_C^3\]\[ = \frac{1}{3}\pi {\left( {\frac{6}{2}} \right)^2}.12 + \frac{1}{2}.\frac{4}{3}.\pi .{\left( {\frac{6}{2}} \right)^3}\]\[ = 54\pi \,\,(c{m^3})\]
Vậy số que kem có thể chia được là: \[\frac{{540\pi }}{{54\pi }} = 10\]que.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.