(1,5 điểm)

Biểu đồ dưới đây biểu diễn kết quả khảo sát thành tích chạy \[100\,{\rm{m}}\] của một số học sinh

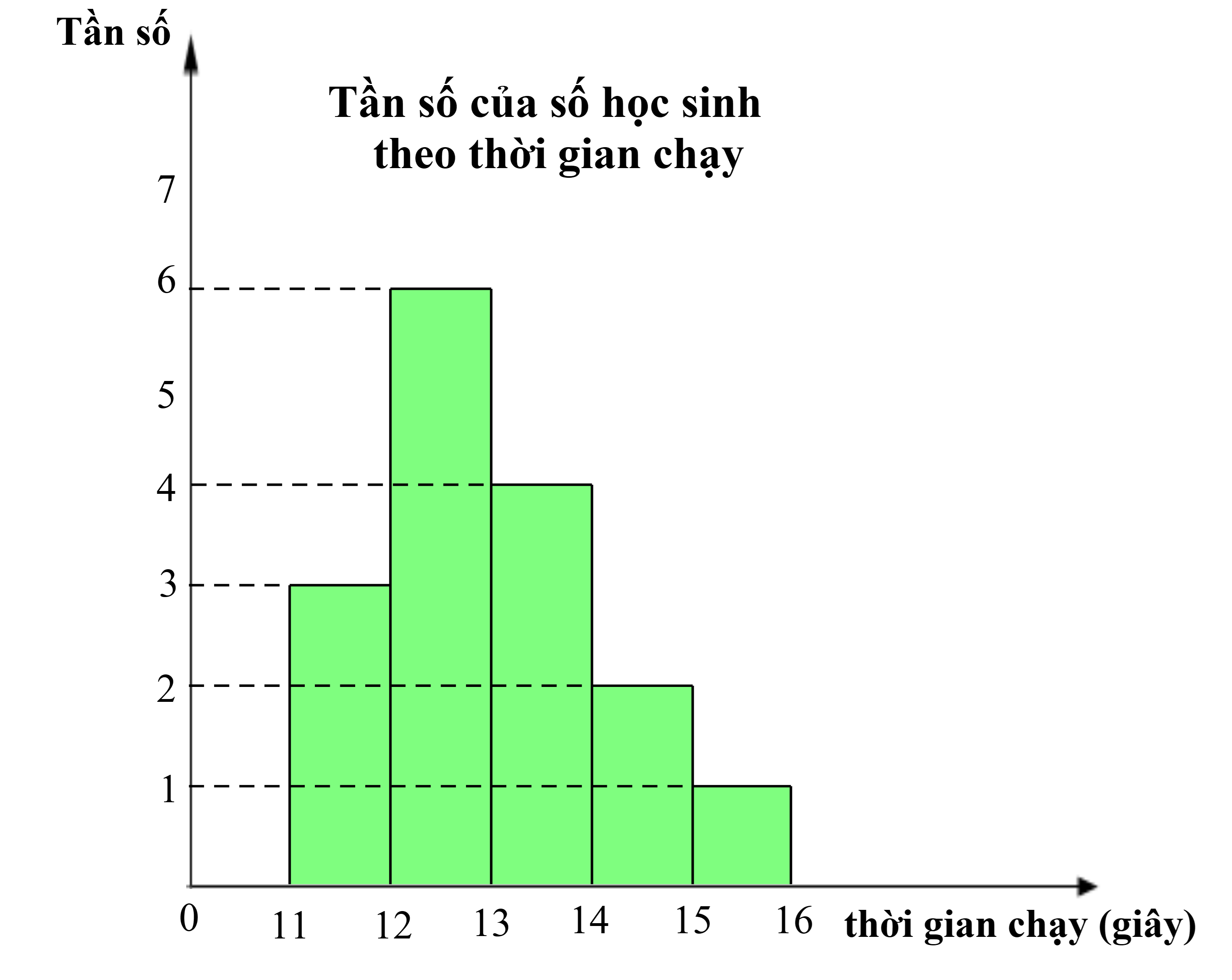
 Có bao nhiêu học sinh chạy \[100\,{\rm{m}}\] hết ít hơn \[13\] giây và tìm tần số tương đối ghép nhóm của nhóm \(\left[ {13;14} \right)\)

 

Gọi thời gian vòi \[I\]chảy một mình đầy bề là \[x\] (giờ \[x > 5\])

Thời gian vòi \[II\] chảy một mình đầy vể là \[y\] (giờ, \[y > 5\])

Thời gian cả hai voi cùng chảy đầy bể là 5 giờ.

Trong 1 giờ, vòi \[I\] chảy được \(\frac{1}{x}\) bể; vòi \[II\] chảy được \(\frac{1}{y}\) bể; cả hai vòi cùng chảy được \(\frac{1}{5}\) bề.

Do đó ta có phương trình: \(\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\)                                                      \(\left( 1 \right)\)

Trong 3 giờ vòi \[I\] chảy được \(\frac{3}{x}\)bề; Trong 2 giờ vòi \[II\] chảy được \(\frac{2}{y}\) bề. Cả hai vòi chảy được \(\frac{2}{3}\) bề.

Do đó ta có phương trình: \(\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\)                                                      \(\left( 2 \right)\)

Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\\\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\end{array} \right.\)

Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}x = 7,5\\y = 15\end{array} \right.\) (thỏa mãn điều kiện).

Vậy:

Thời gian vòi \[I\] chảy một mình đầy bể là 7,5 giờ.

Thời gian vòi \[II\] chảy một mình đẩy bể là 15 giờ.

a) Phần ống nhựa cắm vào phân nửa viên kẹo là hình trụ có độ cao \(h = 0,8\,{\rm{cm}}\), bán kính \(r = 0,2\,{\rm{cm}}\)

Thể tích phần ống nhựa cắm vào phân nửa viên kẹo là:

  \({V_1} = \pi {r^2}h = \pi \,\,.\,\,{0,2^2}\,\,.\,\,1,6 \approx 0,2\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)

 b) Thể tích của viên kẹo tính cả phần ống nhựa cắm vào là:

  \({V_2} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \,\,.\,\,{1,6^3} \approx 17,16\,\left( {{\kern 1pt} {\rm{c}}{{\rm{m}}^3}} \right)\)

  Thể tích thực của viên kẹo sau khi trừ phần ống nhựa:

  \(V = {V_{\rm{2}}} - {V_{\rm{1}}} \approx 17,16 - 0,2 = 16,96\,{\kern 1pt} \left( {{\rm{c}}{{\rm{m}}^3}} \right)\)