(2,5 điểm)
Hai vòi nước cùng chảy vào một cái bể không có nước thì trong 5 giờ sẽ đầy bể. Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ 2 chảy trong 4 giờ thì được \(\frac{2}{3}\) bể nước. Hỏi nếu mỗi vòi nước chảy một mình thì trong bao lâu mới đầy bể.
Hai vòi nước cùng chảy vào một cái bể không có nước thì trong 5 giờ sẽ đầy bể. Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ 2 chảy trong 4 giờ thì được \(\frac{2}{3}\) bể nước. Hỏi nếu mỗi vòi nước chảy một mình thì trong bao lâu mới đầy bể.
Quảng cáo
Trả lời:
Gọi thời gian vòi \[I\]chảy một mình đầy bề là \[x\] (giờ \[x > 5\])
Thời gian vòi \[II\] chảy một mình đầy vể là \[y\] (giờ, \[y > 5\])
Thời gian cả hai voi cùng chảy đầy bể là 5 giờ.
Trong 1 giờ, vòi \[I\] chảy được \(\frac{1}{x}\) bể; vòi \[II\] chảy được \(\frac{1}{y}\) bể; cả hai vòi cùng chảy được \(\frac{1}{5}\) bề.
Do đó ta có phương trình: \(\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\) \(\left( 1 \right)\)
Trong 3 giờ vòi \[I\] chảy được \(\frac{3}{x}\)bề; Trong 2 giờ vòi \[II\] chảy được \(\frac{2}{y}\) bề. Cả hai vòi chảy được \(\frac{2}{3}\) bề.
Do đó ta có phương trình: \(\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\) \(\left( 2 \right)\)
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\\\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\end{array} \right.\)
Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}x = 7,5\\y = 15\end{array} \right.\) (thỏa mãn điều kiện).
Vậy:
Thời gian vòi \[I\] chảy một mình đầy bể là 7,5 giờ.
Thời gian vòi \[II\] chảy một mình đẩy bể là 15 giờ.
Câu hỏi cùng đoạn
Câu 2:
Một xí nghiệp theo kế hoạch phải sản xuất 75 sản phẩm trong một số ngày dự kiến. Trong thực tế, do cải tiến kĩ thuật nên mỗi ngày xí nghiệp làm vượt mức 5 sản phẩm, vì vậy không những họ đã làm được 80 sản phẩm mà còn hoàn thành trước kế hoạch 1 ngày. Hỏi theo kế hoạch, mỗi ngày xí nghiệp sản xuất bao nhiêu sản phẩm?
Gọi số sản phẩm mỗi ngày xí ngiệp phải làm theo kế hoạch là \(x\), (sản phẩm \(x \in \mathbb{N}*,x < 75)\)
Số sản phẩm phải làm theo kế hoạch là 75 sản phẩm.
Thời gian hoàn thành theo kế hoạch là \(\frac{{75}}{x}\) ngày.
Thực tế, mỗi ngày làm được \(x + 5\) sản phẩm.
Thực tế số sản phẩm làm được là 80 sản phẩm.
Thực tế, thời gian hoàn thành là \(\frac{{80}}{x}\) sản phẩm.
Thực tế, xí nghiệp hoàn thành trước 1 ngày so với kế hoạch nên ta có phương trình:
\(\frac{{80}}{{x + 5}} + 1 = \frac{{75}}{x}\)
\(\frac{{80 + x + 5}}{{x + 5}} = \frac{{75}}{x}\)
\({x^2} + 80x + 5x = 75x + 375\)
\({x^2} + 10x - 375 = 0\)
\(\left( {x - 15} \right)\left( {x + 25} \right) = 0\)
Trường hợp 1: \(x = 15 & \left( {{\rm{tho\^u a ma\~o n}}} \right)\)
Trường hợp 2: \(x = - 25\,\left( {{\rm{loa\"i i}}} \right)\)
Vậy, theo kế hoạch mỗi ngày xí nghiệp phải làm 15 sản phẩm.
Câu 3:
Trong mặt phẳng tọa độ \[Oxy\], biết rằng parabol \(y = {x^2}\) và đường thẳng \[\left( d \right):\]\(y = x - m\) có một hoành độ giao điểm là \(x = \frac{{1 - \sqrt 5 }}{2}\). Giả sử \({x_1};{x_2}\) là các hoành độ giao điểm của hai hàm số trên. Không giải phương trình, hãy tính: \(\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} - \frac{{2025}}{{{x_1} + {x_2} - 2}}\).
Hoành độ giao điểm của parabol và đường thẳng \[\left( d \right)\] là nghiệm của phương trình:
\({x^2} = x - m\)
\({x^2} - x + m = 0\)
Hai đồ thị hàm số có một giao điểm là \(x = \frac{{1 - \sqrt 5 }}{2}\) nên ta có:
\({\left( {\frac{{1 - \sqrt 5 }}{2}} \right)^2} - \frac{{1 - \sqrt 5 }}{2} + m = 0\)
\(m = \frac{{1 - \sqrt 5 }}{2} - {\left( {\frac{{1 - \sqrt 5 }}{2}} \right)^2}\)
\( = \frac{{1 - \sqrt 5 }}{2} - \frac{{6 - 2\sqrt 5 }}{4}\)\( = \frac{{1 - \sqrt 5 - 3 + \sqrt 5 }}{2}\)\( = - 1\)
Với \(m = - 1\) ta có phương trình: \({x^2} - x - 1 = 0\)
Theo định lí Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 1\\{x_1}{x_2} = - 1\end{array} \right.\) \(\left( 1 \right)\)
Theo bài ra:\(\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} - \frac{{2025}}{{{x_1} + {x_2} - 2}}\)
\(\frac{{{x_2} + {x_1}}}{{{x_1}{x_2}}} - \frac{{2025}}{{{x_1} + {x_2} - 2}}\) \(\left( 2 \right)\)
Từ (1) và \(\left( 2 \right)\) ta có: \(\frac{1}{{ - 1}} - \frac{{2025}}{{1 - 2}} = - 1 + 2025 = 2024\)
Vậy\(\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} - \frac{{2025}}{{{x_1} + {x_2} - 2}} = 2024\) với \(m =- 1\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
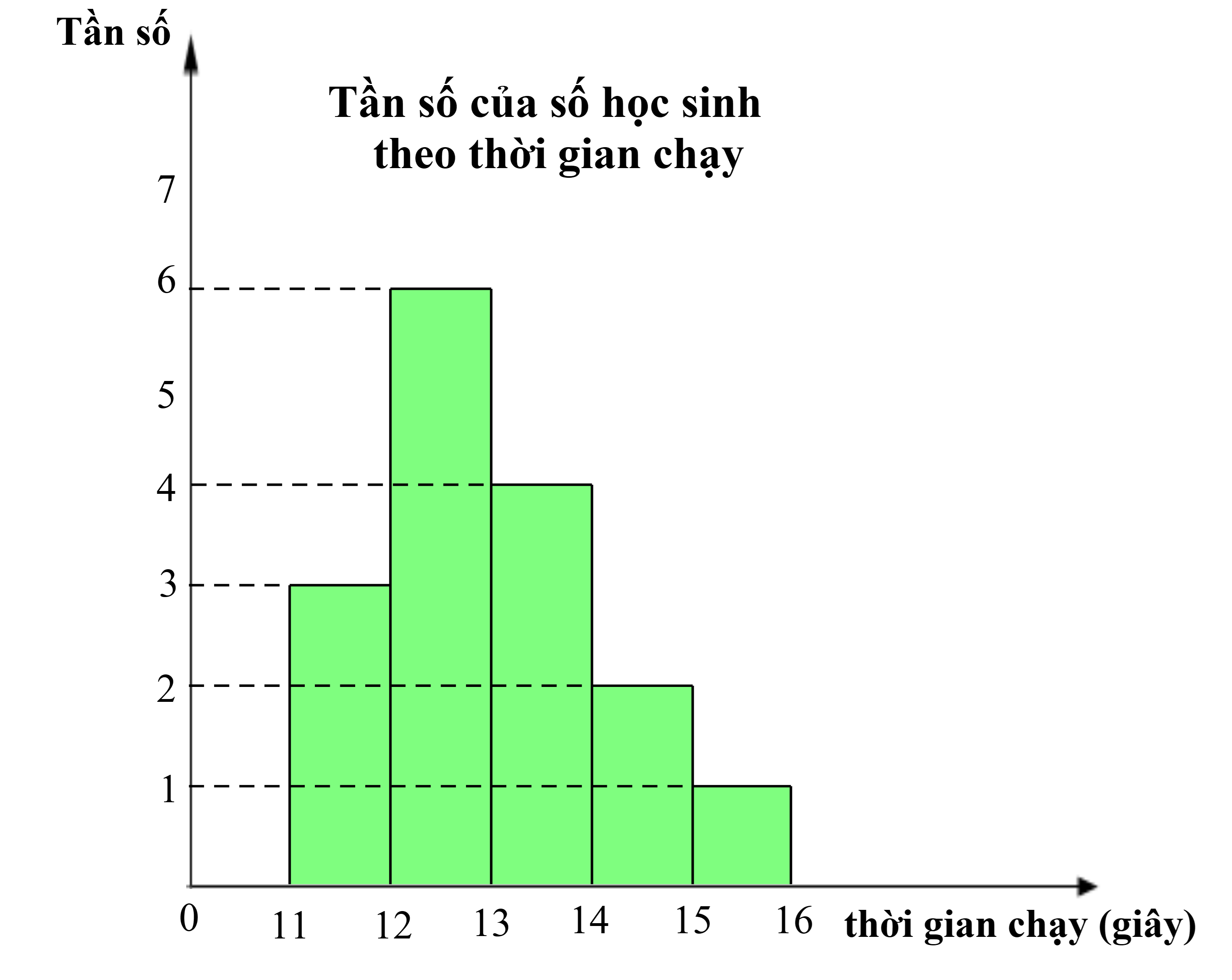
Có \[9\] học sinh chạy \[100\,{\rm{m}}\] hết ít hơn \[13\] giây.
Tần số tương đối ghép nhóm của nhóm \(\left[ {13;14} \right)\) là: \(\frac{4}{{3 + 6 + 4 + 2 + 1}} \cdot 100\% = 25\% \)
Lời giải
a) Phần ống nhựa cắm vào phân nửa viên kẹo là hình trụ có độ cao \(h = 0,8\,{\rm{cm}}\), bán kính \(r = 0,2\,{\rm{cm}}\)
Thể tích phần ống nhựa cắm vào phân nửa viên kẹo là:
\({V_1} = \pi {r^2}h = \pi \,\,.\,\,{0,2^2}\,\,.\,\,1,6 \approx 0,2\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
b) Thể tích của viên kẹo tính cả phần ống nhựa cắm vào là:
\({V_2} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \,\,.\,\,{1,6^3} \approx 17,16\,\left( {{\kern 1pt} {\rm{c}}{{\rm{m}}^3}} \right)\)
Thể tích thực của viên kẹo sau khi trừ phần ống nhựa:
\(V = {V_{\rm{2}}} - {V_{\rm{1}}} \approx 17,16 - 0,2 = 16,96\,{\kern 1pt} \left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.