1. Tính giá trị của biểu thức: \(A = \,\sqrt {27} \, - \,\frac{3}{{\sqrt 3 }}\, - \,\sqrt 3 \).
2. Giải các phương trình và hệ phương trình sau:
a) \({x^2} + 3x - 10 = 0\) b) \({x^4}\, - 8{x^2}\, - 9\, = 0\) c) \(\left\{ \begin{array}{l}3x + y\, = \,2\\x - y\, = 6\end{array} \right.\)
1. Tính giá trị của biểu thức: \(A = \,\sqrt {27} \, - \,\frac{3}{{\sqrt 3 }}\, - \,\sqrt 3 \).
2. Giải các phương trình và hệ phương trình sau:
a) \({x^2} + 3x - 10 = 0\) b) \({x^4}\, - 8{x^2}\, - 9\, = 0\) c) \(\left\{ \begin{array}{l}3x + y\, = \,2\\x - y\, = 6\end{array} \right.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
1. \(A = \,\sqrt {27} \, - \,\frac{3}{{\sqrt 3 }}\, - \,\sqrt 3 \).
\(A\, = \,3\sqrt 3 - \,\sqrt 3 - \sqrt 3 \, = \,2\sqrt 3 \)
2. a) \({x^2} + 3x - 10 = 0\)
\(\Delta \, = \,{3^2} - \,4.1.\left( { - 10} \right) = \,49 > 0\)
Vì \(\Delta > 0\) nên phương trình có hai nghiệm phân biệt:
\({x_1}\, = \,\frac{{ - b + \sqrt \Delta }}{{2a}} = \,\frac{{ - 3 + \sqrt {49} }}{{2.1}}\, = \,2\); \({x_2}\, = \,\frac{{ - b - \sqrt \Delta }}{{2a}} = \,\frac{{ - 3 - \sqrt {49} }}{{2.1}}\, = - 5\)
Vậy tập nghiệm của phương trình: \(S\, = \left\{ {2; - 5} \right\}\).
b) \({x^4}\, - 8{x^2}\, - 9\, = 0\)…(*)
Đặt \(y\, = \,{x^2}\) (Điều kiện: \(y\, \ge 0\))
Khi đó phương trình (*) trở thành: \({y^2}\, - 8y\, - 9 = 0\)…(1)
Vì \(a\, - \,b\, + \,c\, = \,1\, - \left( { - 8} \right) + \left( { - 9} \right) = \,0\) nên phương trình (1) có nghiệm:
\(y = \, - 1\) (loại vì \(y \ge 0\))
\(y\, = \,\frac{{ - c}}{a}\, = 9\)(thỏa \(y \ge 0\)): \({x^2} = 9 \Leftrightarrow \,x\, = \, \pm 3\)
Vậy tập nghiệm của phương trình (*): \(S\, = \,\left\{ { \pm 3} \right\}\).
c) \(\left\{ \begin{array}{l}3x + y\, = \,2\\x - y\, = 6\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}4x = 8\\x - y\, = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2 - y\, = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y\, = - 4\end{array} \right.\)
Vậy tập nghiệm của hệ phương trình: \(S\, = \,\left\{ {\left( {2; - 4} \right)} \right\}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
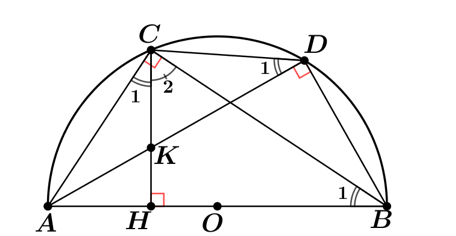
Ta có: \(\widehat {ACB}\, = \,\widehat {ADB}\, = \,{90^0}\)(góc nội tiếp chắn nửa đường tròn đường kính AB).
Suy ra: \(\widehat {KDB\,} = \,{90^0}\)
Vì \(CH\,\, \bot \,\,AB\) nên \(\widehat {CHB\,} = \,{90^0} \Rightarrow \,\widehat {KHB} = \,{90^0}\).
1. Chứng minh BHKD là một tứ giác nội tiếp.
Tứ giác \(BHKD\) có: \(\,\widehat {KHB} + \,\,\widehat {KDB} = \,{90^0}\, + \,{90^0} = {180^0}\)
\( \Rightarrow \) Tứ giác \(BHKD\) là tứ giác nội tiếp.
2. Chứng minh tam giác ACK đồng dạng với tam giác ADC và chứng minh \(AK.\,AD\, = \,A{C^2}\).
Ta có: (góc nội tiếp cùng chắn cung AC)
Mặt khác \(\widehat {{C_1}\,} = \,\widehat {{B_1}}\) (cùng phụ \(\widehat {{C_2}}\))
Do đó \(\widehat {{C_1}\,} = \,\widehat {{D_1}}\)
Xét tam giác ACK và tam giác ADC có:
\(\widehat {CAD}\): góc chung.
\(\widehat {{C_1}\,} = \,\widehat {{D_1}}\)(chứng minh trên)
Vậy: tam giác ACK đồng dạng với tam giác ADC (g – g)
\( \Rightarrow \)\(\frac{{AC}}{{AD}}\, = \,\frac{{AK}}{{AC}}\)\( \Rightarrow AK\,.\,AD\, = \,A{C^2}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \(x\)\(\left( {x > 0;\,\,m} \right)\) là chiều rộng của khu vườn hình chữ nhật.
Suy ra: chiều dài của khu vườn hình chữa nhật là: \(x + 5\,\,\left( m \right)\).
Diện tích khu vườn hình chữ nhật: \(x\left( {x\, + \,5} \right)\,\,\left( {{m^2}} \right)\).
Theo đề bài ta có phương trình: \(x\left( {x\, + \,5} \right)\, = \,150\)
\( \Leftrightarrow {x^2}\, + 5x\, - 150\, = 0\)
Giải phương trình thu được: \({x_1} = \,10\,\,\left( n \right);\,\,{x_2}\, = \, - 15\,\,\left( l \right)\)
Vậy:
Chiều rộng của khu vườn hình chữ nhật là 10 m.
Chiều dài của khu vườn hình chữa nhật là: \(x + 5\, = \,10 + 5\, = 15\,\left( m \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập