Biểu thức \[f\left( x \right) = \frac{{ - {x^2} + x + 6}}{{ - {x^2} + 3x + 4}}\] đạt giá trị dương khi nào?
A. \[x \in \left( { - 2;\, - 1} \right) \cup \left( {3;4} \right)\];
B. \[x \in \left( { - \infty ;\, - 2} \right) \cup \left( {4;\, + \infty } \right)\];
C. \[x \in \left( { - \infty ;\, - 1} \right) \cup \left( {3;\, + \infty } \right)\];
D. \[x \in \left( { - 1;\,3} \right) \cup \left( {4;\, + \infty } \right)\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Tam thức \( - {x^2} + x + 6\) có hai nghiệm là \(x = - 2\) và \(x = 3\);
Tam thức \[ - {x^2} + 3x + 4\] có hai nghiệm \(x = - 1\) và \(x = 4\).
Áp dụng định lí xét dấu, ta có bảng xét dấu sau:
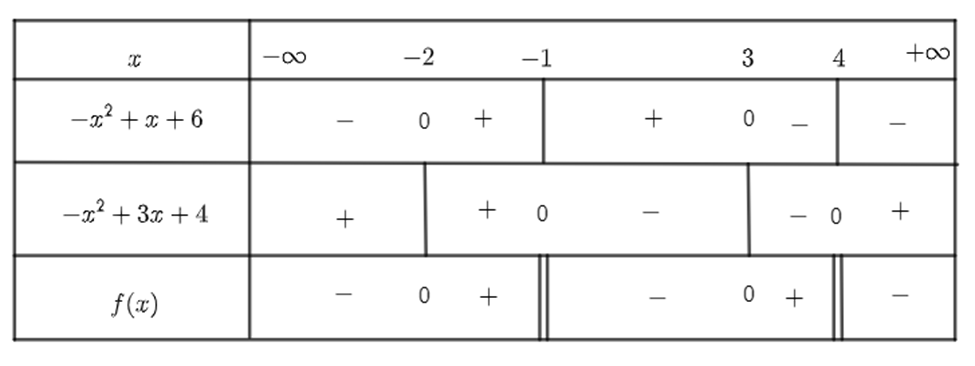
Vậy \[f\left( x \right) = \frac{{ - {x^2} + x + 6}}{{ - {x^2} + 3x + 4}}\] dương khi và chỉ khi \[x \in \left( { - 2;\, - 1} \right) \cup \left( {3;4} \right)\].
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[0 < m < \frac{1}{4}\];
B. \[\frac{{ - 1}}{4} < m < 0\];
C. \[\frac{{ - 1}}{4} < m \le 0\];
D. \[m < - \frac{1}{4}\].
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
+) Với \[m = 0\;\] thì \[f\left( x \right) = - x - 1\] lấy cả giá trị âm và dương (ví dụ \[f\left( { - 2} \right) = 1\]) nên \[m = 0\;\] không thỏa mãn yêu cầu bài toán.
+) Với \[m \ne 0\] thì \[f\left( x \right) = m{x^2} - x - 1\] là tam thức bậc hai, do đó:
\[f\left( x \right) < 0,\,\forall x \Leftrightarrow \left\{ \begin{array}{l}a = m < 0\\\Delta = 1 + 4m < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\m < \frac{{ - 1}}{4}\end{array} \right. \Leftrightarrow m < - \frac{1}{4}\].
Vậy với \[m < - \frac{1}{4}\] thì biểu thức \[f\left( x \right)\] luôn nhận giá trị âm.
Câu 2
A. \[D = \left( {1;\, + \infty } \right)\];
B. \[D = \left( {1;\,6} \right)\];
C. \[D = \left[ {1;\,6} \right]\];
D. \[D = \mathbb{R}\].
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Hàm số xác định khi \[\left\{ \begin{array}{l}6 - x \ge 0\\x - 1 \ge 0\\1 + \sqrt {x - 1} \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 6\\x \ge 1\end{array} \right. \Leftrightarrow 1 \le x \le 6\]
Vậy tập xác định của hàm số là \[D = \left[ {1;\,6} \right]\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[{y_{\min }} = 0\];
B. \[{y_{\min }} = 1\];
C. \[{y_{\min }} = 2\];
D. \[{y_{\min }} = 3\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[4{x^2}\];
B. \[4\];
C. \[6{x^2}\];
D. \[4.\frac{1}{{{x^2}}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập