PHẦN III (5,0 điểm).Tự luận. Thí sinh trình bày bài giải các câu từ câu 15 đến câu 18.

( 1,0 điểm) Giải phương trình \({x^2} - 5x + 6 = 0\).

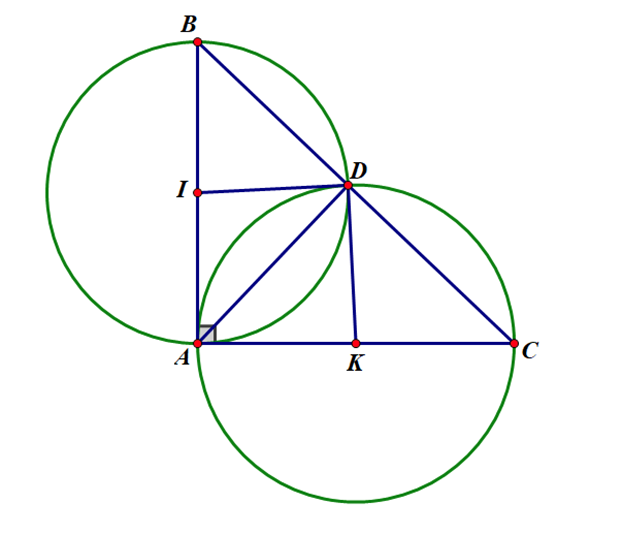
a) Xét đường tròn \(\left( I \right)\) có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Suy ra \(AD \bot \;BD\;\left( 1 \right)\)

Xét đường tròn \(\left( K \right)\) có: \(\widehat {ADC} = 90^\circ \;\) (góc nội tiếp chắn nửa đường tròn)

Suy ra \(AD \bot \;CD\;\left( 2 \right)\)

Từ (1), (2) suy ra \(B,\;C,D\) thẳng hàng nên \(D\) là điểm thuộc cạnh huyền \(BC\).

b) Ta có \({\rm{\Delta }}\;IAK\) vuông tại \(A\)  (\({\rm{\Delta }}\;ABC\) vuông tại \(A\))

Suy ra \({\rm{\Delta }}\;IAK\) nội tiếp đường tròn đường kính \(IK.\)

Suy ra ba điểm \(I,A,K\) thuộc đường tròn đường kính \(IK\)   (3)

Xét đường tròn \(\left( I \right)\) có: \(IA = ID\) (cùng bán kính)

Suy ra \({\rm{\Delta }}\;IAD\) cân tại I nên \(\widehat {IAD} = \widehat {IDA}\;\;\left( * \right)\)

Xét đường tròn \(\left( K \right)\) có: \(KA = KD\) (cùng bán kính)

Suy ra \({\rm{\Delta }}\;IAD\) cân tại I nên \(\widehat {KAD} = \widehat {KDA}\;\;\left( {**} \right)\)

Ta có \(\widehat {IAD} + \widehat {KAD} = \widehat {IAK\;} = 90^\circ \,\,\left( {***} \right)\)

Từ (*), (**), (***) suy ra \(\widehat {IDK\;} = \widehat {IDA\;} + \widehat {KDA} = 90^\circ \)

Nên \({\rm{\Delta }}\;IDK\) vuông tại \(D\)

Suy ra \({\rm{\Delta }}\;IDK\) nội tiếp đường tròn đường kính \(IK.\)

Suy ra ba điểm \(I,D,K\) thuộc đường tròn đường kính \(IK\)  (4)

Từ (3) và (4) suy ra \(A,I,D,K\) cùng thuộc một đường tròn.

Vậy tứ giác \(AIDK\) là tứ giác nội tiếp.

a) Bảng tần số:

b) Giá trị có tần số lớn nhất là 2,5 kg.

Tần số tương đối: \(f = \frac{{12}}{{40}}.100\% = 30\% \)