(1,0 điểm):

Trong ngày thứ nhất, tổng doanh thu của hai hãng taxi A và B là \(90\) triệu đồng, sang ngày thứ hai thì tổng doanh thu của hai hãng taxi trên là \(93\) triệu đồng. Biết rằng trong ngày thứ hai, doanh thu của hãng A tăng \(20\% \)còn doanh thu của hãng B thì giảm \(10\% \) so với ngày thứ nhất. Hỏi doanh thu của mỗi hãng trong ngày thứ nhất là bao nhiêu triệu đồng?

Gọi số lần tăng giá một chiếc áo là \(x\) (nghìn đồng), \(x \ge 0\).

Vì mỗi lần tăng 20 nghìn đồng nên giá bán mới cho mỗi chiếc áo là \(P = 330 + 20x\) (nghìn đồng)

Số lượng áo bán được khi tăng giá là \(13\,\,500 - 900x\) (cái).

Lợi nhuận khi bán một chiếc áo là \(330 + 20x - 190 = 140 + 20x\) (nghìn đồng)

Tổng lợi nhụn thu được khi täng giá là: \(\left( {13500 - 900x} \right) \cdot \left( {140 + 20x} \right)\) (nghìn đồng)

Ta có

\(\begin{array}{l}\left( {13\,\,500 - 900x} \right).\left( {140 + 20x} \right)\\ =  - 18\,\,000{x^2} + 144\,\,000x + 1\,\,890\,\,000\\ =  - 18\,\,000\left( {{x^2} - 8x} \right) + 1\,\,890\,\,000\\ =  - 18\,\,000\left[ {{{\left( {x - 4} \right)}^2} - 10} \right] + 1\,\,890\,\,000\end{array}\)

\( =  - 18\,\,000.{\left( {x - 4} \right)^2} + 2\,\,178\,\,000 \le 2\,\,178\,\,000\) vì \( - 18\,\,000{(x - 4)^2} \le 0,x \in \mathbb{R}\).

Suy ra tổng lợi nhuận thu được lớn nhất bằng \[1\,\,278\,\,000\].

Dấu "=" xảy ra khi \(x = 4\) (lần)

Vậy số lần tăng giá một chiếc áo là 4 lần và giá bán mỗi chiếc áo là \(P = 330 + 20.4 = 410\) (nghìn đồng).

a) Chứng minh bốn điểm \[B,C,E,F\]cùng thuộc một đường tròn.

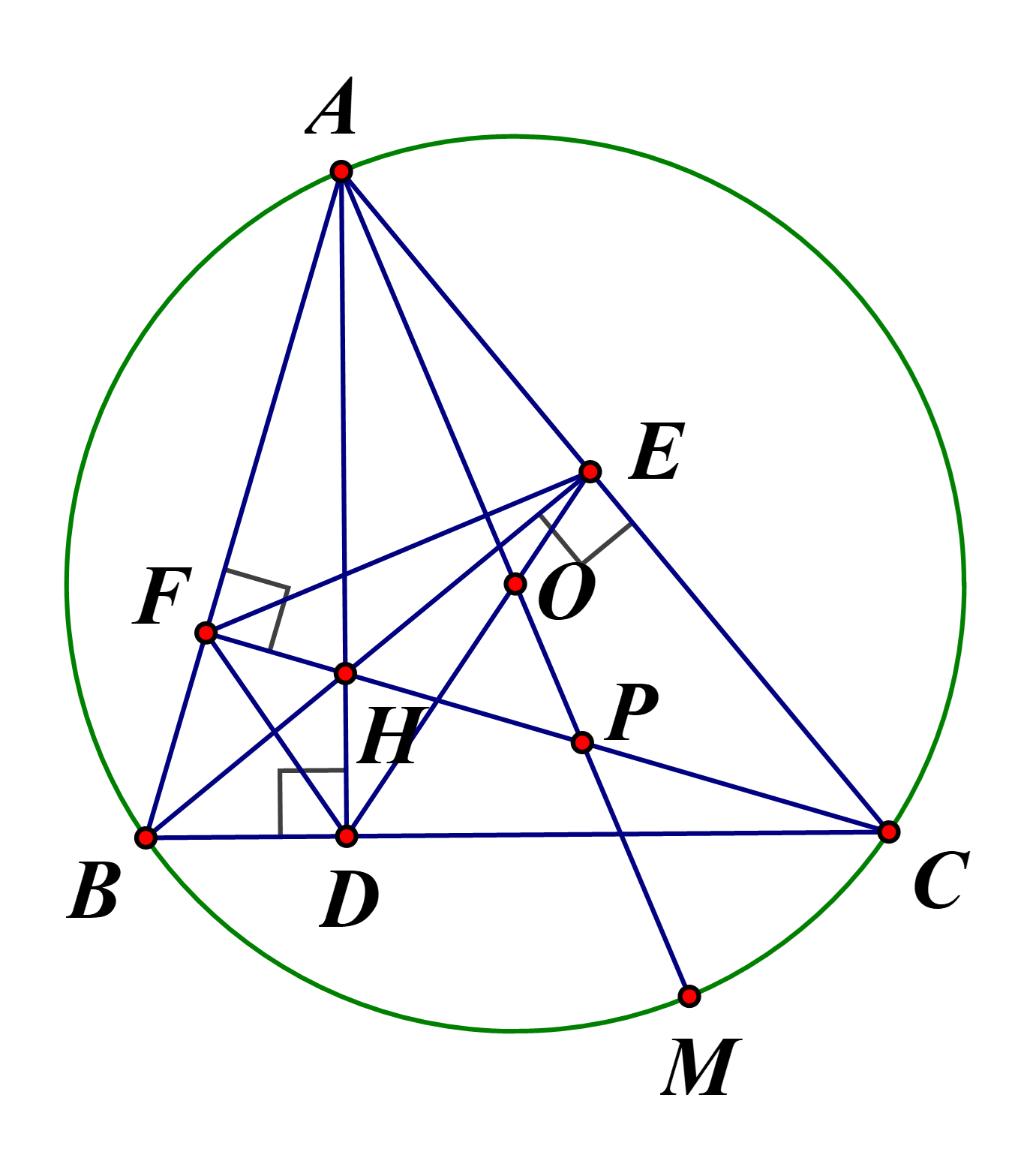
 Vì \(BE,\,CF\)là hai đường cao của \(\Delta ABC\)nên \(BE \bot AC,\,\,\,CF \bot AB\).

Do\(\Delta BEC\) vuông tại \(E\) nên 3 điểm \(B,E,C\) cùng thuộc đường tròn đường kính \(BC\).

Do\(\Delta BFC\) vuông tại \(F\) nên 3 điểm \(B,F,C\) cùng thuộc đường tròn đường kính \(BC\).

Vậy 4 điểm \[B,C,E,F\] cùng thuộc đường tròn đường kính \(BC\).

                 b) Gọi \(D\) là giao điểm của \(AH\) và \(BC\). Đường kính \(AM\)của đường tròn \(\left( O \right)\)cắt đường thẳng  

                 \(CF\)tại điểm \(P\). Chứng minh  \(\widehat {BAD} = \widehat {CAM}\) và \(AP.BH = AH.CP\).

                 Do \(AM\) là đường kính nên \(\widehat {ABM} = \widehat {ACM} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

                 Ta có \(\widehat {BAD} + \widehat {ABD} = 90^\circ \) (vì \(\Delta ABD\)vuông tại \(D\)) và \(\widehat {CAM} + \widehat {AMC} = 90^\circ \) (vì \(\Delta ACM\)vuông tại \(C\))       Mà \(\widehat {ABD} = \widehat {AMC}\) (góc nội tiếp cùng chắn cung \(AC\)) nên suy ra \(\widehat {BAD} = \widehat {CAM}\)

                 Xét \(\Delta APC\)và \(\Delta AHB\) có:

                 \(\widehat {BAD} = \widehat {CAM}\,\,\,(cmt)\)

                 \(\widehat {ABH} = \widehat {ACP}\,\,\,\)(góc nội tiếp cùng chắn cung \(EF\))

                 Suy ra

                 Nên \(\frac{{AP}}{{AH}} = \frac{{PC}}{{HB}}\) hay \(AP.HB = AH.PC\)

                 c) Gọi \(I\) là trung điểm của \(BC\), đường thẳng\(AI\)cắt \[EF\]tại \(K\). Gọi \(N\)là hình chiếu vuông góc

                 của \(K\) trên \(BC\). Chứng minh \(AN\)đi qua trung điểm của \[EF\].

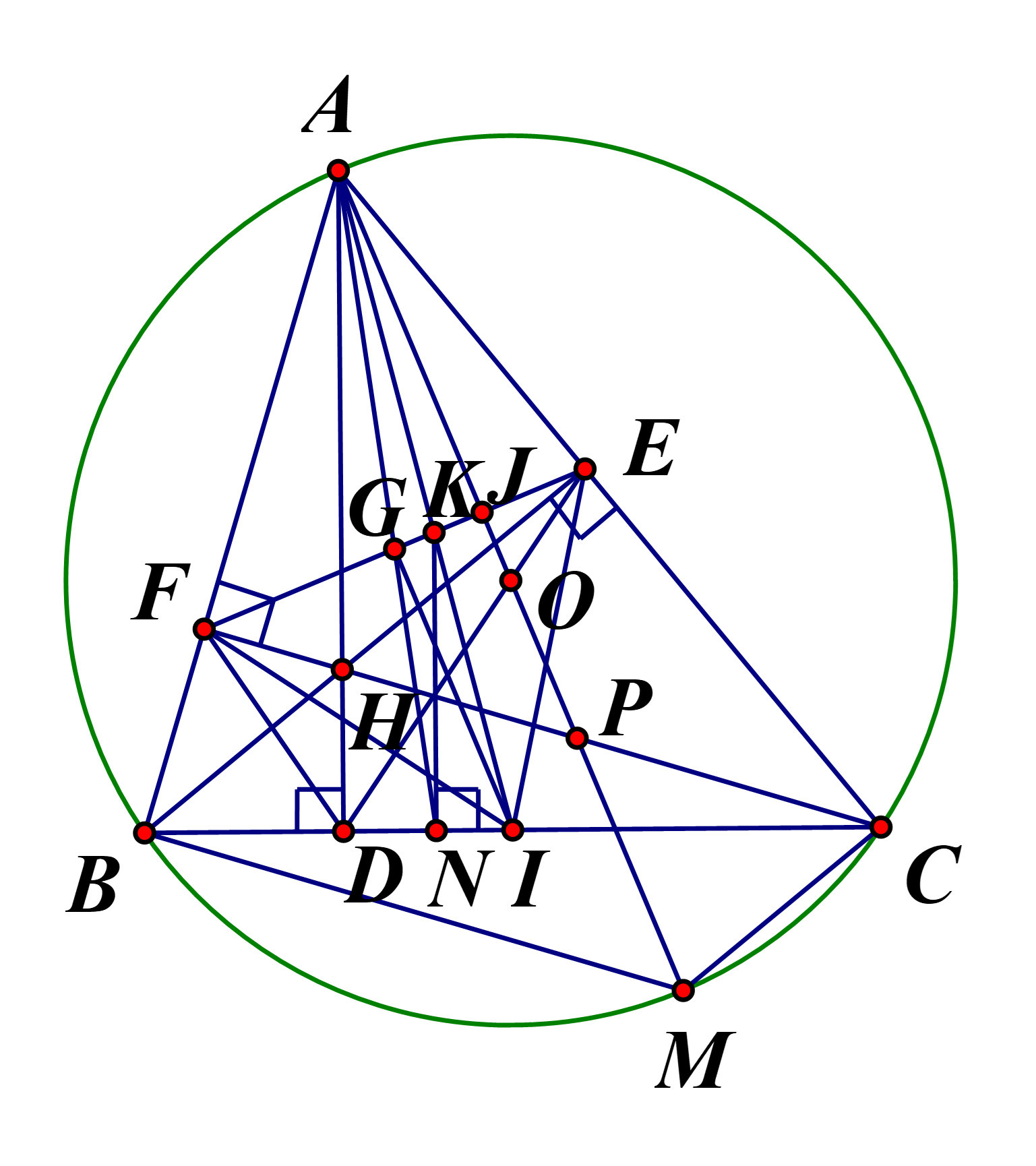
Gọi \(G\) là trung điểm của \[EF\], \(J\) là giao điểm của \[AM\]và \[EF\], \[AG\] cắt \(BC\) tại \(N'\).

Ta sẽ chứng minh \[KN' \bot BC\].

Ta có: \[\widehat {AEJ} + \widehat {EAJ} = \,\,\,\widehat {ABC} + \widehat {CBM} = \widehat {ABM} = 90^\circ \] nên \(\Delta AJE\)vuông tại \(J\).

Do  nên \(\frac{{A\,E}}{{AB}} = \frac{{AF}}{{AC}} = \frac{{EF}}{{BC}} = \frac{{2GF}}{{2IC}} = \frac{{GF}}{{IC}}\,\,\,\,\,\left( 1 \right)\)

Kết hợp với \(\widehat {AFG} = \widehat {ACI}\)(cùng cộng \(\widehat {BFE}\) bằng \(180^\circ \,).\)

Suy ra

Khí đó \(\widehat {BAG} = \widehat {KAE}\,\,\,\)và \(\frac{{AG}}{{AI}} = \frac{{AF}}{{AC}}\,\,\,\,\,\,\left( 2 \right)\)

Tương tự ta có   (do \(\widehat {BAG} = \widehat {KAE}\)và \(\widehat {AEK} = \widehat {ABI}\))

Nên \(\frac{{AK}}{{AN'}} = \frac{{AE}}{{AB}}\,\,\,\,\,\left( 3 \right)\)

Từ (1), (2) và (3) suy ra \(\frac{{AG}}{{AI}} = \frac{{AK}}{{AN'}}\,\,\,\,\)

Mà \[\widehat {N'AI}\] chung nên suy ra \(\widehat {AN'K} = \widehat {AIG}\,\,\,\,\,\,\,\left( 4 \right)\)

\(\Delta IEF\)cân tại \(I\) (do \[IE = IF\]) có \(IG\)là đường trung tuyến nên cũng đồng thời là đường cao.

Suy ra \(IG\)//\(AO\)(vì cùng vuông góc với \[EF\]). Do đó \(\widehat {GIA} = \widehat {IAO}\,\)(so le trong)

Lại có \(\widehat {BAG} = \widehat {KAE}\,\,\left( {cmt} \right)\) và \(\widehat {FAH} = \widehat {JAE}\,\,\left( {cmt} \right)\)nên \[\widehat {IAO}\, = \widehat {GAH}\]

Suy ra \(\widehat {GIA} = \widehat {GAH}\,\,\,\,\,\,\left( 5 \right)\)

Từ (4) và (5) suy ra \(\widehat {AN'K} = \widehat {GAH}\,\)nên \(KN'\)//\(AD\) (so le trong)

Mà \(AD \bot BC\)nên\(KN' \bot BC\). Ta lại có \(KN \bot BC\,\,\left( {gt} \right)\)

Suy ra \(N' \equiv N\)hay \(AN\)đi qua trung điểm \(G\)của \[EF\]. (đpcm)