Một cái cổng được thiết kế dạng parabol có phương trình biểu diễn trong hệ trục tọa độ Oxy là \({\rm{y}} = a{{\rm{x}}^2}\) (với a là hằng số khác 0). Biết khoảng cách giữa hai chân cổng \({\rm{AB}}\) là \(6\;{\rm{m}}\), chiều cao từ điểm chính giữa cổng đến mặt đất \(OI = 4,5\;{\rm{m}}\).


a) Tìm hệ số \(a\) dựa vào dữ kiện đã cho.
b) Một xe tải có chiều rộng bằng \(2\;{\rm{m}}\), chiều cao bằng \(3,2\;{\rm{m}}\) đi vào chính giữa cổng trên. Hỏi xe tải có đi qua được cổng này mà không chạm vào cổng hay không? Giải thích lý do.
Một cái cổng được thiết kế dạng parabol có phương trình biểu diễn trong hệ trục tọa độ Oxy là \({\rm{y}} = a{{\rm{x}}^2}\) (với a là hằng số khác 0). Biết khoảng cách giữa hai chân cổng \({\rm{AB}}\) là \(6\;{\rm{m}}\), chiều cao từ điểm chính giữa cổng đến mặt đất \(OI = 4,5\;{\rm{m}}\).


a) Tìm hệ số \(a\) dựa vào dữ kiện đã cho.
b) Một xe tải có chiều rộng bằng \(2\;{\rm{m}}\), chiều cao bằng \(3,2\;{\rm{m}}\) đi vào chính giữa cổng trên. Hỏi xe tải có đi qua được cổng này mà không chạm vào cổng hay không? Giải thích lý do.
Quảng cáo
Trả lời:
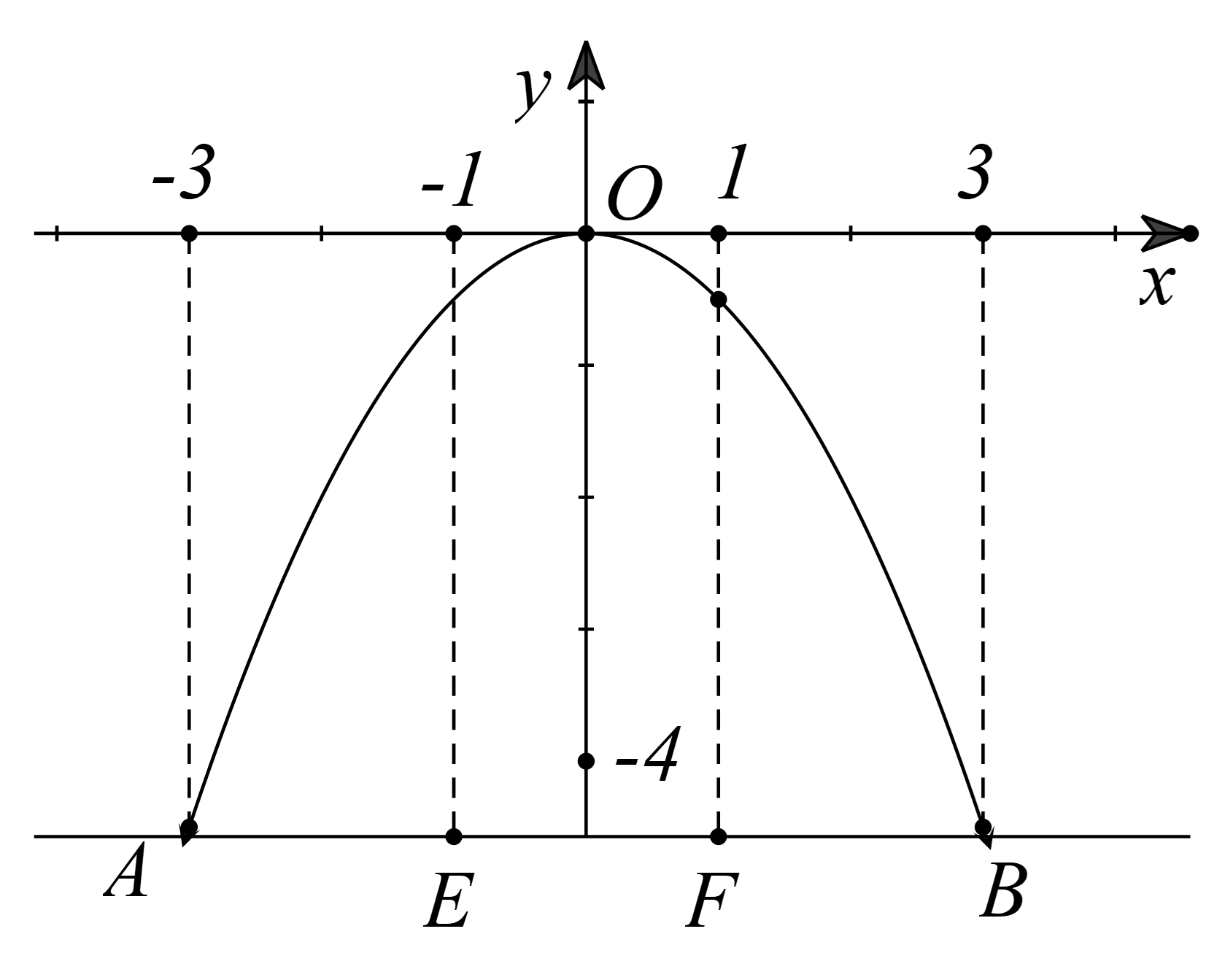
a) Vì parabol đi qua điểm \(A\left( { - 3; - 4,5} \right)\)nên ta có:
\( - 4,5 = x.{( - 3)^2}\)
\(a = \frac{{ - 4,5}}{{{{\left( { - 3} \right)}^2}}}\) = \(\frac{{ - 1}}{2}\)
Vậy hệ số \(a = \frac{{ - 1}}{2}\;\).
b) Chiếc xe tải có chiều rộng bằng 2m nên khoảng cách \(EI = IF = \frac{2}{2} = 1\;{\rm{m}}\).
Với \({\rm{x}} = 1\) thì y = \(y = \frac{{ - 1}}{2} \cdot {1^2}\) = \(\frac{{ - 1}}{2}\) nên chiều cao tối đa của chiếc xe có thể đi qua cổng là:\(4,5 - \left| {\frac{{ - 1}}{2}} \right| = 4,5 - 0,5 = 4\) > 3,2
Vậy xe tải này có thể đi được qua cổng đó mà không chạm vào cổng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
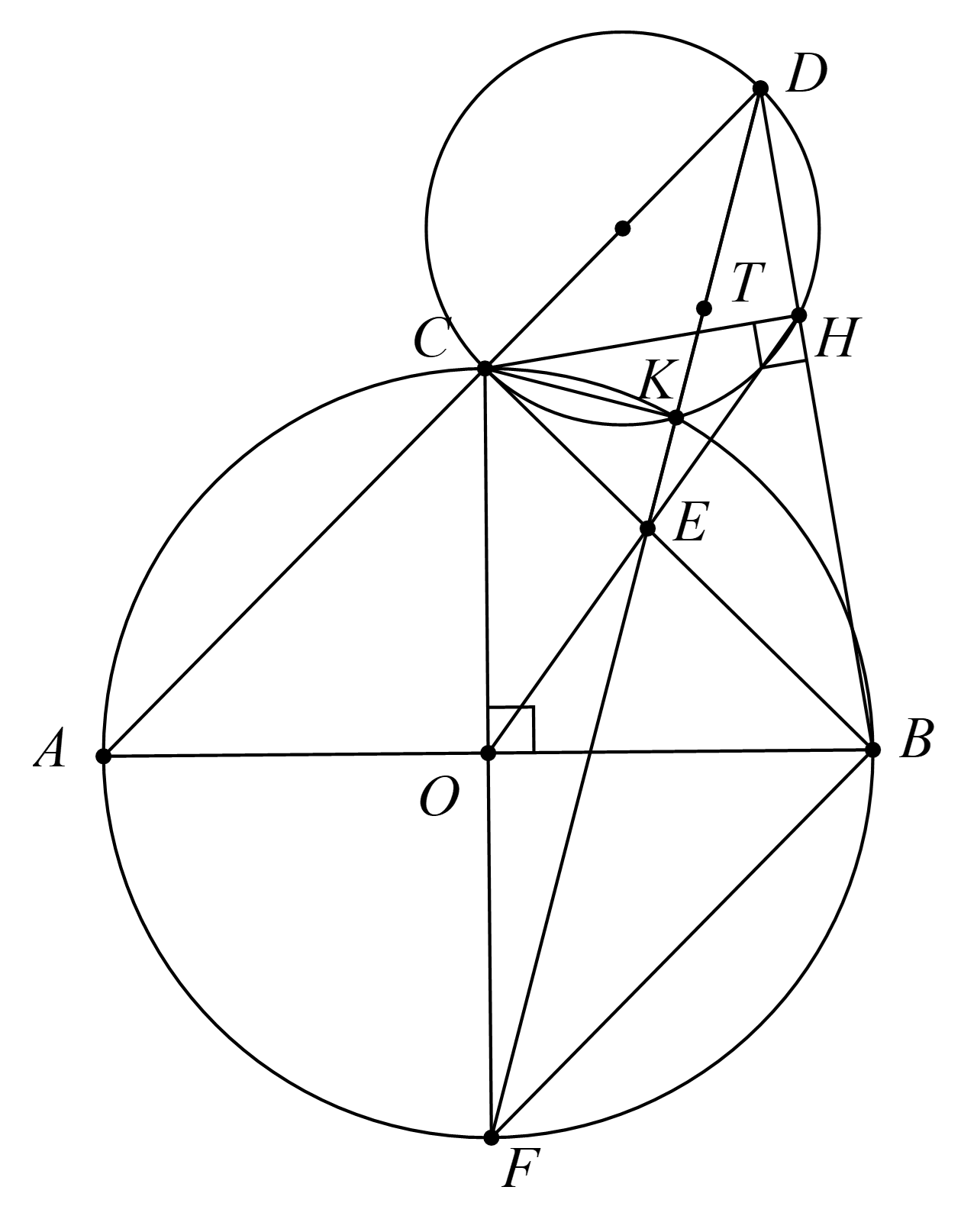
a) Xét \(\Delta {\rm{OCB}}\)vuông tại \(O\) nên \(\Delta {\rm{OCB}}\) nội tiếp đường tròn đường kính \({\rm{CB}}\)
Xét \({\rm{\Delta HCB}}\)vuông tại \(H\) nên \(\Delta H{\rm{CB}}\) nội tiếp đường tròn đường kính \({\rm{CB}}\)
Do đó tứ giác \({\rm{OBHC}}\)nội tiếp đường tròn đường kính \({\rm{CB}}\).
b)
theo chứng minh phần a ta có tứ giác \({\rm{OBHC}}\)nội tiếp đường tròn đường kính \({\rm{CB}}\)
suy ra \(\widehat {CHO} = \widehat {CBA} = 45^\circ \) (cùng chắn cung \(OC\))
Nên \(\widehat {OHB} = \widehat {CHB} - \widehat {CHO} = 90^\circ - 45^\circ = 45^\circ \)
Do đó \({\rm{HO}}\) là tia phân giác của \(\widehat {CHB}\) .
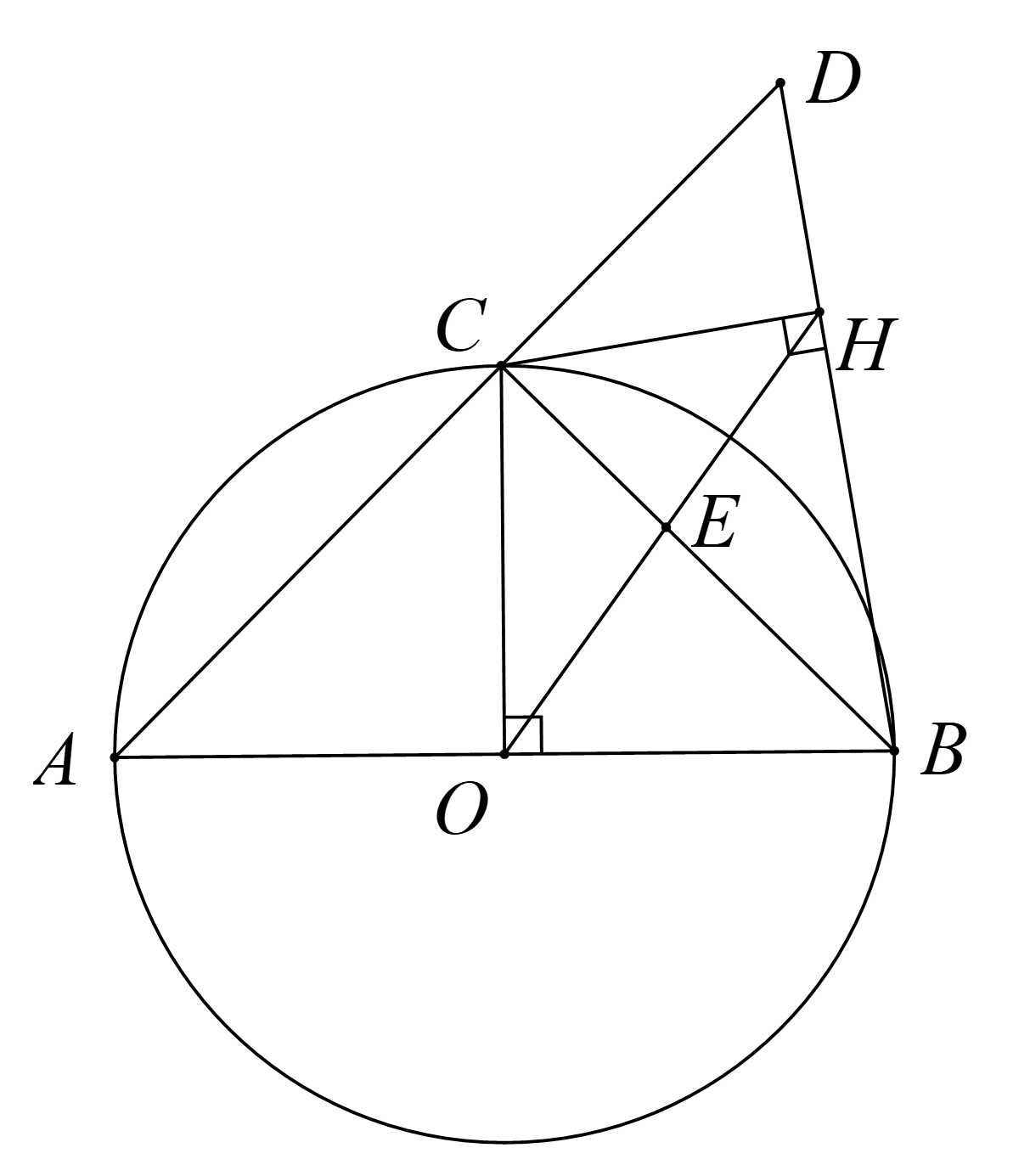
Xét \(\left( O \right)\) có \(\widehat {ACB} = 90^\circ \) góc nội tiếp chắn nửa đường tròn.
Xét \(\Delta CBD\) vuông tại \(C\), có đường cao \(AH\) nên \(C{H^2} = HB.HD\) hay \(\frac{{HC}}{{HB}} = \frac{{HD}}{{HC}}\)
Mặt khác \({\rm{HO}}\) là tia phân giác của \(\widehat {CHB}\) nên \(\frac{{HC}}{{HB}} = \frac{{CE}}{{BE}}\)
Do đó \(\frac{{HD}}{{HC}} = \frac{{CE}}{{BE}}\) hay \({\rm{CE}}{\rm{.CH = BE}}{\rm{.HD}}\).
c) 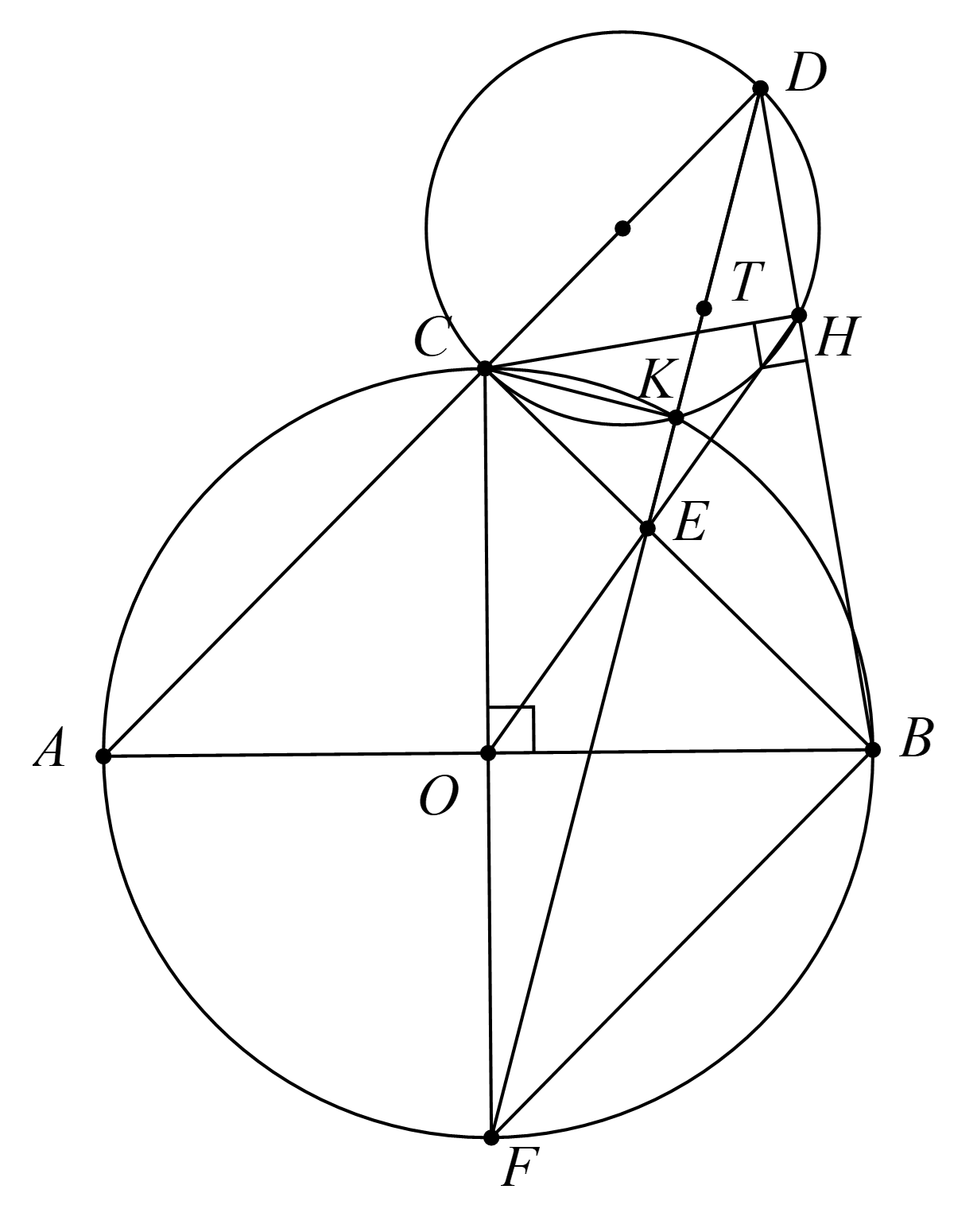
Vì \(CD\)là đường kính của đường tròn ngoại tiếp \(\Delta {\rm{CHD}}\)
\({\rm{CE}} \bot {\rm{CD}}\) suy ra \({\rm{CE}}\) là tiếp tuyến của đường tròn ngoại tiếp \(\Delta {\rm{CHD}}\)
Gọi \({\rm{CF}}\) là đường kính của \(\left( {\rm{O}} \right)\)
Ta có \(\widehat {{\rm{CHD}}} = \widehat {{\rm{CKF}}} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Do đó \({\rm{F}}{\rm{,}}\;{\rm{K}}{\rm{,}}\;{\rm{D}}\) thẳng hàng
Mặt khác \(\widehat {{\rm{CBF}}} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Suy ra \(CD\;{\rm{//}}\;BF\)
Theo cmpa ta có \(\frac{{{\rm{CE}}}}{{{\rm{BE}}}}{\rm{ = }}\frac{{{\rm{HD}}}}{{{\rm{CH}}}}\)
Do đó \(\Delta {\rm{CHD}}\) đồng dạng với \(\Delta {\rm{BCD}}\) (g.g)
Nên \(\frac{{{\rm{HD}}}}{{{\rm{CH}}}} = \frac{{{\rm{CD}}}}{{{\rm{BC}}}}{\rm{ = }}\frac{{{\rm{CD}}}}{{{\rm{BF}}}}\)
Suy ra \(\frac{{{\rm{CE}}}}{{{\rm{BE}}}}{\rm{ = }}\frac{{{\rm{CD}}}}{{{\rm{BF}}}}\)
Xét hai tam giác \(\Delta {\rm{DCE}}\) và \(\Delta {\rm{BFE}}\)
\(\widehat {{\rm{DCE}}}{\rm{ = }}\widehat {{\rm{FBE}}} = 90^\circ \)
\(\widehat {{\rm{CDE}}}{\rm{ = }}\widehat {{\rm{BFE}}}\) (hai góc so lê trong)
Do đó \(\Delta {\rm{DCE}}\) đồng dạng với \(\Delta {\rm{BFE}}\) (g.g)
Từ đó \(\widehat {{\rm{CED}}}{\rm{ = }}\widehat {{\rm{BEF}}}\)suy ra \(\widehat {{\rm{CEF}}}{\rm{ + }}\widehat {{\rm{CED}}}{\rm{ = }}\widehat {{\rm{CEF}}}{\rm{ + }}\widehat {{\rm{BEF}}} = 180^\circ \)
Hay \({\rm{D}}{\rm{,}}\;{\rm{E}}{\rm{,}}\;{\rm{F}}\) thẳng hàng
Do đó \({\rm{D}}{\rm{,}}\;{\rm{E}}{\rm{,}}\;{\rm{K}}\) thẳng hàng
Xét tam giác \({\rm{CED}}\) vuông tại \({\rm{C}}\)có \({\rm{CK}}\) là đường trung tuyến ứng với cạnh huyền\({\rm{DE}}\).
Gọi \({\rm{T}}\) là trung điểm của \({\rm{DE}}\) thì \({\rm{CT}} = \frac{1}{2}{\rm{DE}}\)
Do đó \({\rm{CK}} \le {\rm{CD}} = \frac{1}{2}{\rm{DE}}\) hay \(2.\;{\rm{CD}} \le {\rm{DE}}\)
Dấu “=” xảy ra khi tam giác \({\rm{CED}}\) vuông cân tại \({\rm{C}}\)
Suy ra \(\widehat {{\rm{ECK}}} = 45^\circ \) hay \(\widehat {{\rm{BOK}}} = 90^\circ \) do đó \({\rm{K}} \equiv {\rm{C}}\) (không xảy ra)
Vậy \({\rm{DE}} > 2.\;{\rm{CK}}\)
Câu 2
Lời giải
Đáp án đúng là D
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.\[20\sqrt 2 \;m\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
