Cho đường tròn \(\left( O \right)\), bán kính \(R(R > 0)\) và dây cung \(BC = R\sqrt 3 \). Lấy một điểm \(A\) bất kì trên cung lớn \(BC\) sao cho tam giác \(ABC\) có ba góc nhọn. Các đường cao \(AD,BE\) của tam giác \(ABC\) cắt nhau tại \(H\).

a)   Chứng minh rằng tứ giác \(DHEC\) nội tiếp.

b)  Kẻ đường kính \(AM\) của đường tròn \(\left( O \right)\) và \(OI\) vuông góc với \(BC\) tại \(I\). Chứng minh rằng \(I\) là trung điểm của \(HM\).

c)   Khi \(DH \cdot DA\) lớn nhất, hãy tính diện tích tam giác \(ABC\) theo \(R\).

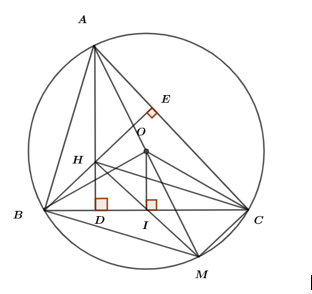
a)   Chứng minh rằng tứ giác \(DHEC\) nội tiếp.

Xét tam giác \(ABC\) có

+) \(BE\) là đường cao ứng với \(AC\) \[ \Rightarrow BE \bot AC\]tại \(E\)

\[ \Rightarrow \widehat {HEC} = 90^\circ  \Rightarrow \Delta HEC\]vuông tại \(E\). Suy ra điểm \(H;E;C\)thuộc đường tròn đường kính \(HC\) (1)

+) \(AD\) là đường cao ứng với \(BC\) \[ \Rightarrow AD \bot BC\] tại \(D\)

\[ \Rightarrow \widehat {HDC} = 90^\circ  \Rightarrow \Delta HDC\] vuông tại \(D\). Suy ra điểm \(H;D;C\)thuộc tròn đường kính \(HC\) (2)

Từ (1) và (2) ta có \(H;D;C;E\) nằm trên đường tròn đường kính \(HC\).

Khi đó tứ giác \(DHEC\) nội tiếp.

b)  Kẻ đường kính \(AM\) của đường tròn \(\left( O \right)\) và \(OI\) vuông góc với \(BC\) tại \(I\). Chứng minh rằng \(I\) là trung điểm của \(HM\).

Xét tam giác \(ABC\) có hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\), suy ra \(H\) là trực tâm \[ \Rightarrow CH \bot AB\]

Xét đường tròn \(\left( O \right)\) có \[\widehat {ACM} = 90^\circ \]( góc nội tiếp chắn nửa đường tròn) \[ \Rightarrow CM \bot AC\]

Có \[BE \bot AC \Rightarrow BE{\rm{//}}CM \Rightarrow BH{\rm{//}}CM\].

Tương tự \[\widehat {ABM} = 90^\circ \](góc nội tiếp chắn nửa đường tròn) \[ \Rightarrow BM \bot AB\]

Có \[CH \bot AB(cmt) \Rightarrow BM{\rm{//}}CH\].

Xét tứ giác \(BHCM\) có \[BH{\rm{//}}CM\];\[BM{\rm{//}}CH\] nên tứ giác \(BHCM\)là hình bình hành.

*) Chứng minh \(I\) là trung điểm BC

Xét tam giác OBC có \(OB = OC = R\), suy ra tam giác \(OBC\) cân tại \(O\).

Mà  \[OI \bot BC\,\] (gt)

 Nên \(OI\) là đường cao đồng thời là trung tuyến của tam giác \(OBC\).

Suy ra \(IB = IC\)

Hình bình hành \(BHCM\) có \(I\) là trung điểm của đường chéo \(BC\)

Suy ra \(I\) là trung điểm của \(HM\).

c)   Khi \(DH \cdot DA\) lớn nhất, hãy tính diện tích tam giác \(ABC\) theo \(R\).

*)   Xét \[\Delta BHD\,\,v\`a \,\,\Delta ACD\]có

\[\widehat {BDH} = \widehat {ADC} = 90^\circ \]

\[\widehat {HBD} = \widehat {DAC}\]( cùng phụ với \[\widehat {ACB}\])

\[ \Rightarrow DH.AD = BD.CD \le \frac{{{{(BD + CD)}^2}}}{4} = \frac{{B{C^2}}}{4} = \frac{{3{R^2}}}{4}\]

Dấu “=” xảy ra khi \(DB = DC\). Mà \[AD \bot BC\]tại \(D\)

Suy ra, Tam giác \(ABC\) cân tại \(A\) và \(D\) trùng với \(I\)   (3)

*) \(I\) là trung điểm của \(BC\) \[ \Rightarrow BI = IC = \frac{{BC}}{2} = \frac{{R\sqrt 3 }}{2}\]

\[\Delta OBI\]vuông tại \(I\) có

\[\begin{array}{l}\sin \widehat {BOI} = \frac{{BI}}{{OB}} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {BOI} = 60^\circ \\ \Rightarrow \widehat {BOC} = 2\widehat {BOI} = 2.60^\circ  = 120^\circ \\X\'e t\,\,(O):\,\,\widehat {BAC} = \frac{1}{2}\widehat {BOC} = 60^\circ \,\,\,\,\,\,\,(4)\,\end{array}\]

Từ (3) và (4) ta suy ra Tam giác \(ABC\) đều

\[A{D^2} + B{D^2} = A{B^2} \Rightarrow A{D^2} = A{B^2} - B{D^2} = 3{R^2} - \frac{{3{R^2}}}{4} = \frac{{9{R^2}}}{4} \Rightarrow AD = \frac{{3R}}{2}(AD > 0)\]

\[{S_{\Delta ABC}} = \frac{1}{2}AD.BC = \frac{1}{2}.\frac{{3R}}{2}.R\sqrt 2  = \frac{{3\sqrt 3 }}{4}{R^2}\]

\[ \Rightarrow \Delta ABD\,\]vuông tại D:  Theo định lí Pythagore có

\[A{D^2} + B{D^2} = A{B^2} \Rightarrow A{D^2} = A{B^2} - B{D^2} = 3{R^2} - \frac{{3{R^2}}}{4} = \frac{{9{R^2}}}{4} \Rightarrow AD = \frac{{3R}}{2}(AD > 0)\]

\[{S_{\Delta ABC}} = \frac{1}{2}AD.BC = \frac{1}{2}.\frac{{3R}}{2}.R\sqrt 2  = \frac{{3\sqrt 3 }}{4}{R^2}\]