1. Tính giá trị của biểu thức \[P = {x^{2022}} - 10{x^{2021}} + {x^{2020}} + 2021\] tại \(x = \frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt 3 + \sqrt 2 }}\).
2. Giải phương trình: \(x + \sqrt {{x^2} - 1} = \sqrt {x + 1} + \sqrt {x - 1} + 4\).
3. Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^3} + 3x = {y^3} - 8\\{x^2} + {y^2} = y + 2\end{array} \right.\).
1. Tính giá trị của biểu thức \[P = {x^{2022}} - 10{x^{2021}} + {x^{2020}} + 2021\] tại \(x = \frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt 3 + \sqrt 2 }}\).
2. Giải phương trình: \(x + \sqrt {{x^2} - 1} = \sqrt {x + 1} + \sqrt {x - 1} + 4\).
3. Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^3} + 3x = {y^3} - 8\\{x^2} + {y^2} = y + 2\end{array} \right.\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
1. Tính giá trị của biểu thức \[P = {x^{2022}} - 10{x^{2021}} + {x^{2020}} + 2021\] tại \(x = \frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt 3 + \sqrt 2 }}\) .
Ta có: \(x = \frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt 3 + \sqrt 2 }} = \frac{{{{\left( {\sqrt 3 - \sqrt 2 } \right)}^2}}}{{\left( {\sqrt 3 + \sqrt 2 } \right)\left( {\sqrt 3 - \sqrt 2 } \right)}}\)
\( = \frac{{5 - 2\sqrt 6 }}{{3 - 2}} = 5 - 2\sqrt 6 \).
Suy ra: \({\left( {x - 5} \right)^2} = 24 \Rightarrow {x^2} - 10x + 1 = 0\).
Do đó, \[P = {x^{2020}}\left( {{x^2} - 10x + 1} \right) + 2021 = 2021\].
2. Giải phương trình: \(x + \sqrt {{x^2} - 1} = \sqrt {x + 1} + \sqrt {x - 1} + 4\).
Điều kiện: x ³ 1. Đặt \(t = \sqrt {x + 1} + \sqrt {x - 1} \) ( \(t \ge \sqrt 2 \)).
Suy ra: \({t^2} = 2x + 2\sqrt {{x^2} - 1} \).
Phương trình thành: \(\frac{{{t^2}}}{2} = t + 4 \Leftrightarrow {t^2} - 2t - 8 = 0 \Leftrightarrow t = 4\) (nhận) hoặc t = -2 (loại).
Khi đó, \(\sqrt {x + 1} + \sqrt {x - 1} = 4 \Leftrightarrow \sqrt {{x^2} - 1} = 8 - x\)
Û \(\left\{ \begin{array}{l}x \le 8\\{x^2} - 1 = 64 - 16x + {x^2}\end{array} \right. \Leftrightarrow x = \frac{{65}}{{16}}\) (nhận).
Vậy tập nghiệm của phương trình là: \(S = \left\{ {\frac{{65}}{{16}}} \right\}\).
3. Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^3} + 3x = {y^3} - 8\,\,\,\left( 1 \right)\\{x^2} + {y^2} = y + 2\,\,\,\,\,\left( 2 \right)\end{array} \right.\).
Lấy phương trình (2) nhân 3 hai vế cộng với phương trình (1) ta được:
\({\left( {x + 1} \right)^3} = {\left( {y - 1} \right)^3} \Leftrightarrow x + 1 = y - 1 \Leftrightarrow y = x + 2\).
Thế vào phương trình (2) ta được: \[{x^2} + {\left( {x + 2} \right)^2} = \left( {x + 2} \right) + 2 \Leftrightarrow 2{x^2} + 3x = 0\]
Û \(x = - \frac{3}{2}\) hoặc x = 0.
· TH1: x = 0 Þ y = 2.
· TH2: \(x = - \frac{3}{2}\) Þ \(y = \frac{1}{2}\).
Vậy tập nghiệm của hệ phương trình là: \(S = \left\{ {\left( {0;2} \right),\left( { - \frac{3}{2};\frac{1}{2}} \right)} \right\}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đặt \(d = \left( {m,n} \right)\). Khi đó, \(m = d{m_1},\,\,n = d{n_1}\), \(\left( {{m_1},{n_1}} \right) = 1\), \({m_1},{n_1} \in {\mathbb{Z}^ + }\).
Ta có: \(mn|{m^2} + {n^2} + m\)
\( \Rightarrow {d^2}{m_1}{n_1}|{d^2}m_1^2 + {d^2}n_1^2 + d{m_1} \Rightarrow d|d{m_1}{n_1}|dm_1^2 + dn_1^2 + {m_1} \Rightarrow d|{m_1}\).
Tương tự \[{m_1}|d{m_1}{n_1}|dm_1^2 + dn_1^2 + {m_1} \Rightarrow {m_1}|dn_1^2 \Rightarrow {m_1}|d\], vì \(\left( {{m_1},{n_1}} \right) = 1\).
Do đó, \(d = {m_1}\) Þ \(m = {d^2}\) là số chính phương.
Lời giải
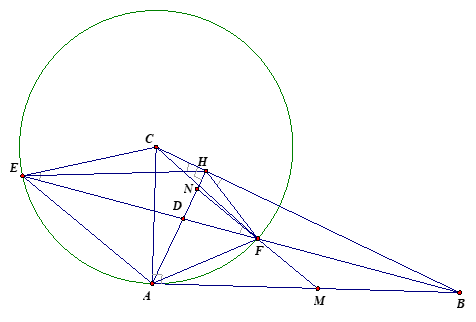
a) Chứng minh BH.BC = BE.BF .
Ta có: (g.g) vì có \(\widehat {ABF}\) chung và \(\widehat {BAF} = \widehat {AEB}\) (cùng chắn cung ).
Suy ra: \(\frac{{BA}}{{BE}} = \frac{{BF}}{{BA}} \Rightarrow BE.BF = B{A^2}\).
Theo hệ thức lượng trong tam giác vuông ABC ta có: \(B{A^2} = BH.BC\) Þ BH.BC = BE.BF.
b) Chứng minh HD là tia phân giác của góc \(\widehat {EHF}\).
Ta có: (c.g.c) vì có \(\widehat {HBF}\) chung và \(\frac{{BH}}{{BE}} = \frac{{BF}}{{BC}}\) (suy từ câu a).
Suy ra: \(\widehat {BHF} = \widehat {BEC}\) (1) Þ tứ giác EFHC nội tiếp đường tròn.
Do đó, \(\widehat {EHC} = \widehat {EFC}\) (cùng chắn cung )
= \(\widehat {CEF}\) (do D CEF cân tại C). (2)
Từ (1) và (2) Þ \(\widehat {FHB} = \widehat {EHC}\)
Þ \(\widehat {DHE} = \widehat {DHC} - \widehat {EHC} = 90^\circ - \widehat {EHC} = \widehat {DHB} - \widehat {FHB} = \widehat {DHF}\).
Do đó, HD là tia phân giác của góc \(\widehat {EHF}\).
c) Chứng minh F là trung điểm MN.
Vì MF// AE nên theo định lý Ta-lét ta có: \(\frac{{MF}}{{AE}} = \frac{{BF}}{{BE}}\).(3)
Vì NF// AE nên theo định lý Ta-lét ta có: \(\frac{{NF}}{{AE}} = \frac{{DF}}{{DE}}\). (4)
Xét D EHF có HD ^ HB và HD là tia phân giác trong của góc \(\widehat {EHF}\)nên HB là tia phân giác ngoài của góc \(\widehat {EHF}\)Þ \(\frac{{BF}}{{BE}} = \frac{{HF}}{{HE}} = \frac{{DF}}{{DE}}\). (5)
Từ (3), (4), (5) Þ \(\frac{{MF}}{{AE}} = \frac{{NF}}{{AE}}\) Þ MF = NF Þ F là trung điểm MN.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập