Bên trong một biển quảng cáo hình tròn tâm \(O\) đường kính 70 cm , người thợ vẽ hai đường tròn \(\left( {{O_1}} \right),\left( {{O_2}} \right)\) có cùng bán kính, tiếp xúc ngoài với nhau và cùng tiếp xúc trong với đường tròn \(\left( O \right)\) để trang trí (tham khảo hình vẽ). Tính (theo \({\rm{c}}{{\rm{m}}^2}\)) diện tích nhỏ nhất của phần thuộc hình tròn \(\left( O \right)\) mà không thuộc hai hình tròn \(\left( {{O_1}} \right),\left( {{O_2}} \right)\) (phần không tô đen), làm tròn kết quả đển hàng đơn vị.

Gọi \(x\) là số đơn vị mới được sáp nhập từ 2 đơn vị cũ và \(y\) là số đơn vị mới được sáp nhập từ 3 đơn vị cũ. Điều kiện \(x,y\) nguyên dương.

Tổng số đơn vị mới là: \(x + y + 2 + 4 = 36\) hay \(x + y = 30\) (1)

Tổng số đơn vị trước khi sáp nhập là: \(2x + 3y + 2.5 + 4.4 = 94\) hay \(2x + 3y = 68\)(2)

Từ (1) và (2) tìm được \(x = 22,y = 8\) (thoả điều kiện).

Vậy có 22 đơn vị mới được sáp nhập từ 2 đơn vị cũ và 8 đơn vị mới được sáp nhập từ 3 đơn vị cũ.

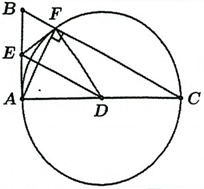
Ta có \(\widehat {EAD} = {90^ \circ }\) nên \(A,E,D\) cùng thuộc đường tròn đường kính \(ED\) (1)

\(\Delta AFB\) vuông tại \(F\) có \(FE\) là đường trung tuyến nên \(FE = EB = EA\).

Do đó \(\Delta EBF\) cân tại \(E\). Suy ra \(\widehat {EBF} = \widehat {EFB}\).

\(\widehat {DFC} = \widehat {DCF}\) (\(\Delta DFC\) cân tại \(D\) ) và \(\widehat {EBF} + \widehat {DCF} = 90^\circ \).

Suy ra \(\widehat {EFB} + \widehat {DFC} = 90^\circ \) hay \(\widehat {EFD} = 90^\circ \).

Do đó \(E,F,D\) cùng thuộc đường tròn đường kính \(ED\) (2)

Từ (1) và (2) suy ra \(A,E,F,D\) cùng thuộc một đường tròn đường kính \(ED\).