Cho nửa đường tròn tâm \(O\), đường kính \(AB\). Trên nửa đường tròn \(\left( O \right)\) lấy điểm \(C\) sao cho \(CA < CB\), kẻ \(CD\) vuông góc với \(AB\), \(D\) thuộc \(AB\). Gọi \(F\) là một điểm trên đoạn \(CD\) ( \(F\) khác \(C\) và \(D\) ), tia \(AF\) cắt nửa đường tròn \(\left( O \right)\) tại \(E\).
a) Chứng minh tứ giác \[DFEB\] là tứ giác nội tiếp.
b) Gọi \(M\), \(N\) lần lượt là chân đường vuông góc kẻ từ \(O\) xuống \(AE\) và \(BF\); \(H\) là giao điểm cùa \(BE\) và \(DF\); \(I\) là trung diểm cùa \(HF\). Chứng minh \(OI\) đi qua trung điểm của \[MN\] ,
a) Chứng minh tứ giác \[DFEB\] là tứ giác nội tiếp.
b) Gọi \(M\), \(N\) lần lượt là chân đường vuông góc kẻ từ \(O\) xuống \(AE\) và \(BF\); \(H\) là giao điểm cùa \(BE\) và \(DF\); \(I\) là trung diểm cùa \(HF\). Chứng minh \(OI\) đi qua trung điểm của \[MN\] ,
Quảng cáo
Trả lời:
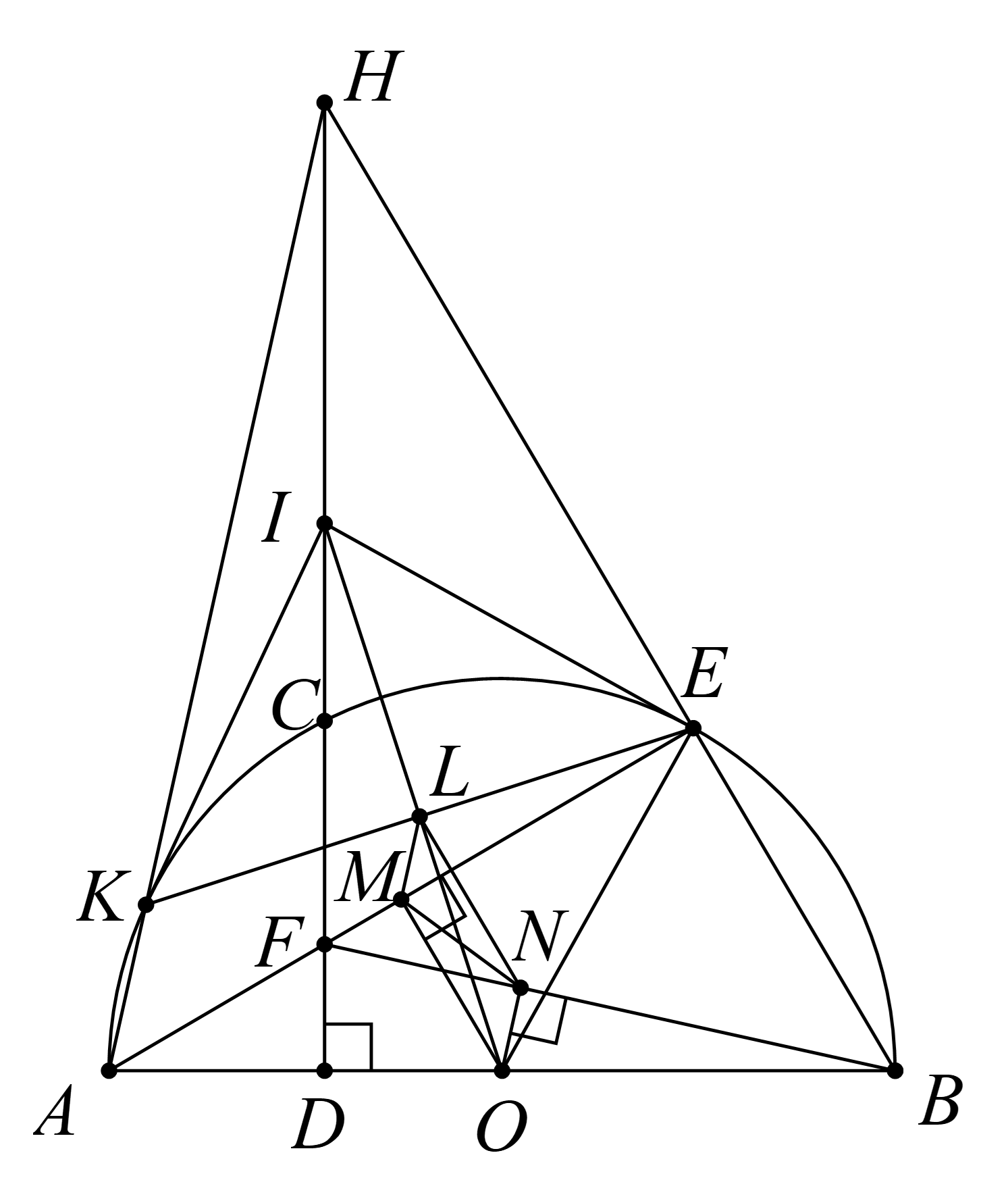
a) Chứng minh tứ giác \[DFEB\] là tứ giác nội tiếp.
Ta có \(DF \bot AB\) nên \(\Delta DFB\) vuông tại \[D\]
Suy ra \(D\), \(F\), \(B\) cùng thuộc đường tròn đường kính \[FB\]
Ta có \(\widehat {AEB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta FBE\) vuông tại \[E\]
Suy ra \(D\), \(E\), \(B\) cùng thuộc đường tròn đường kính \[FB\]
Vậy \(D\), \(E\), \(B\), \(F\) cùng thuộc đường tròn đường kính \[FB\] hay \[DFEB\] là tứ giác nội tiếp.
b) Chứng minh \(OI\) đi qua trung điểm của \[MN\].
Gọi \(K\) là giao điểm của \(HA\) và \(\left( O \right)\)
Khi đó \(AE\), \(HD\), \(BK\) là các đường cao của tam giác \(HAB\)
Do đó \(AE\), \(HD\), \(BK\) đồng quy tại \(F\) hay \(B\), \(F\), \(K\) thẳng hàng
Vì \(\Delta HKF\) vuông tại \(K\), \(\Delta HEF\) vuông tại \(E\) nên \(H\), \(K\), \(F\), \(E\) cùng thuộc đường tròn đường kính \(HF\)
Suy ra \(KI = IE\)
Do đó \(I\) thuộc đường trung trực của \(EK\)
Mà \(O\) thuộc đường trung trực của \(EK\) (do \(OE = OK\) )
Nên \(OI\) là trung trực của \(EK\)
Gọi \(L\) là giao điểm của \(OI\) và \(EK\). Khi đó \(L\) là trung điểm của \(EK\)
Mà \(M\) là trung điểm của \(AE\) nên \(ML\) là đường trung bình của \(\Delta AKE\)
Do đó \(ML\,{\rm{//}}\,AK\), \(ML = \frac{1}{2}AK\;\;\left( 1 \right)\)
Tương tự \(ON\,{\rm{//}}\,AK\), \(ON = \frac{1}{2}AK\;\;\left( 2 \right)\)
Từ (1) và (2) suy ra \[MLNO\] là hình bình hành
Do đó \(OL\) đi qua trung điểm của \(MN\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi vận tốc của Lan khi đi xe đạp từ A đến B là \(x{\rm{\;}}\left( {{\rm{km/h}}} \right)\). ĐK \(x > 0\)
Vận tốc của Lan lúc về là \(x + 2\;\left( {{\rm{km/h}}} \right)\)
Thời gian đi từ \(A\) đến \(B\) là \(\frac{{20}}{x}\) (giờ)
Thời gian đi từ \(B\) về \(A\) là \(\frac{{20}}{{x + 2}}\) (giờ)
Vì thời gian về ít hơn thời gian đi \[20\] phút hay \(\frac{1}{3}\) giờ nên ta có phương trình: \(\frac{{20}}{x} - \frac{{20}}{{x + 2}} = \frac{1}{3}\)
\(\frac{{60\left( {x + 2} \right)}}{{3x\left( {x + 2} \right)}} - \frac{{60x}}{{3x\left( {x + 2} \right)}} = \frac{{x\left( {x + 2} \right)}}{{3x\left( {x + 2} \right)}}\)
Suy ra \(60\left( {x + 2} \right) - 60x = x\left( {x + 2} \right)\)
\(60x + 120 - 60x = {x^2} + 2x\)
\({x^2} + 2x - 120 = 0\)
\({x^2} + 12x - 10x - 120 = 0\)
\(x\left( {x + 12} \right) - 10\left( {x + 12} \right) = 0\)
\(\left( {x - 10} \right)\left( {x + 12} \right) = 0\)
\(x - 10 = 0\) hoặc \(x + 12 = 0\)
\(x = 10\) (tmĐK) hoặc \(x = - 12\) (không tmĐK)
Vậy vận tốc của Lan khi đi xe đạp từ A đến B là \(10{\rm{\;km/h}}\).
Lời giải
a) Tính diện tích xung quanh của chiếc cốc (lấy \(\pi = 3,14\) )
Diện tích xung quanh của chiếc cốc là \({S_{xq}} = 2\pi rh\)\( = 2\pi \;{\rm{.}}\;5\;{\rm{.}}\;10\)\( = 314\;\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)
Vậy diện tích xung quanh của chiếc cốc là \(314\;\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)
b) Ban đầu chiếc cốc chứa nước, chiều cao mục nước là \({h_1} = 6{\rm{\;cm}}\). Người ta thả một viên bi bằng sắt, đặc ruột, hình cầu có bán kính \(R = 3{\rm{\;cm}}\) vào chiếc cốc. Khi đó chiều cao của mục nước trong cốc là \({h_2}\). Tính \({h_2}\)
b) Thể tích của viên bi sắt là \({V_1} = \frac{4}{3}\pi {R^3}\)\( = \frac{4}{3}\pi \;{\rm{.}}\;{3^3}\)\( = 36\pi \;\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\)
Thể tích nước trong cốc ban đầu là \(V = \pi {r^2}h\)\( = \pi \;{\rm{.}}\;{5^2}\;{\rm{.}}\;6\)\( = 150\pi \;\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\)
Tổng thể tích của viên bi sắt và nước ban đầu là \({V_2} = V + {V_1}\)\( = 150\pi + 36\pi \)\( = 186\pi \;\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\)
Chiều cao của mực nước sau khi thả viên bi là \({h_2} = \frac{{{V_2}}}{{\pi {r^2}}}\)\( = \frac{{186\pi }}{{\pi \cdot {5^2}}}\)\( = 7,44\;\left( {{\rm{cm}}} \right)\)
Vậy \({h_2} = 7,4{\rm{4}}\;\left( {{\rm{cm}}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
