Parabol ở hình vẽ bên là đồ thị của hàm số nào?
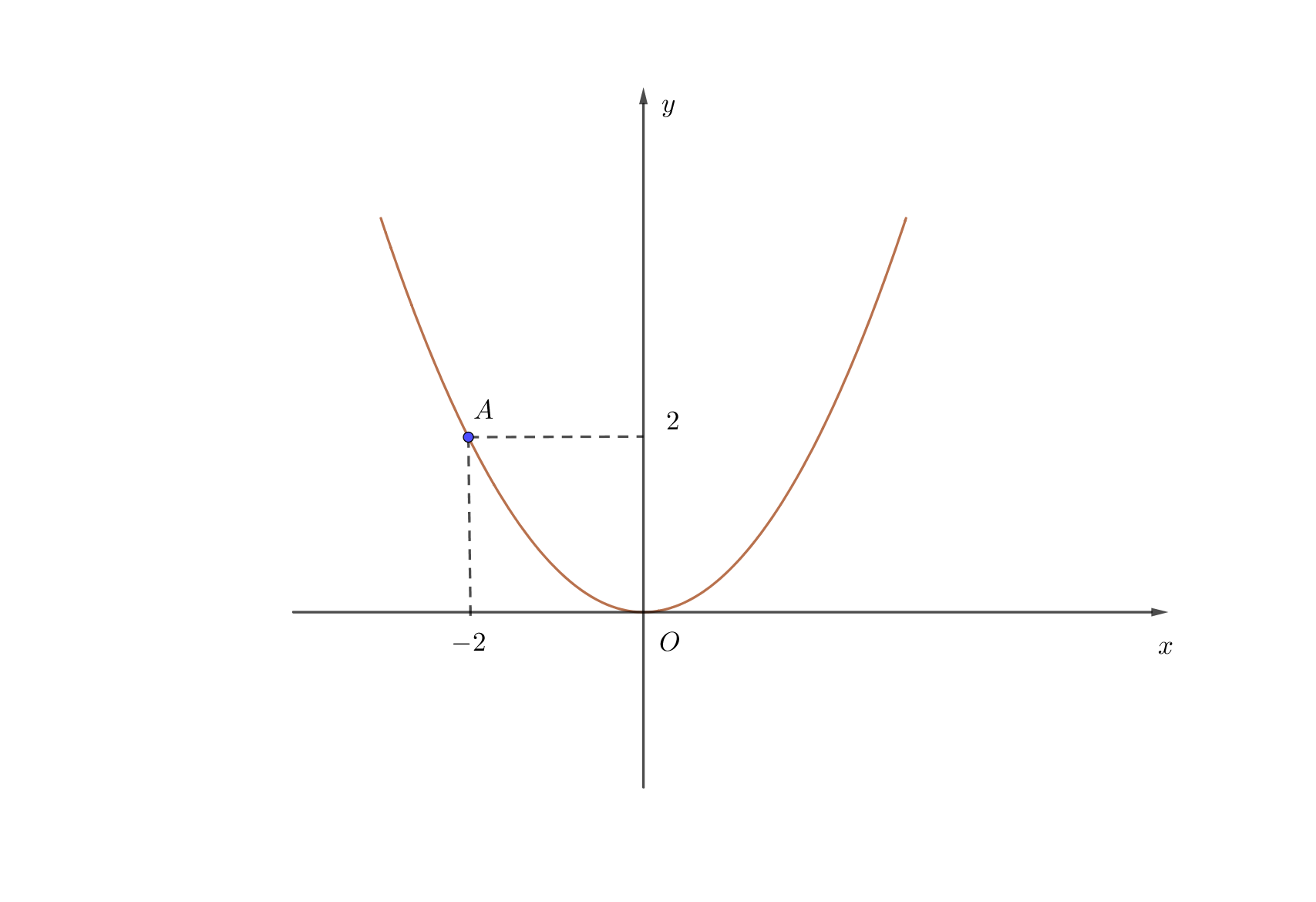
Parabol ở hình vẽ bên là đồ thị của hàm số nào?

Quảng cáo
Trả lời:
Chọn C
Cách 1: Parabol đã cho có dạng là đồ thị hàm số \[y = a{x^2}\left( {a > 0} \right)\].
Do parabol này đi qua điểm \[A\left( { - 2\,;\,2} \right)\] nên \[a.{\left( { - 2} \right)^2} = 2\]\[ \Leftrightarrow a = \frac{1}{2}\] ( thỏa mãn \[a > 0\]).
Vậy hàm số cần tìm là \[y = \frac{1}{2}{x^2}\].
Cách 2: Parabol đã cho có dạng là đồ thị hàm số \[y = a{x^2}\left( {a > 0} \right)\] nên ta có thể loại ngay phương án D.
Thử trực tiếp các phương án còn lại, nhận thấy hàm số có đồ thị đi qua điểm \[A\left( { - 2\,;\,2} \right)\] là \[y = \frac{1}{2}{x^2}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn A
Điểm thuộc \(\left( P \right)\) có tung độ bằng \( - 6\) thì hoành độ \(x\) thỏa mãn phương trình \( - 6 = - 2{x^2}\) nên \({x^2} = 3.\)
Do đó \(x = 3\) hoặc \(x = - 3.\)
Vậy tọa độ các điểm cần tìm là \(\left( {\sqrt 3 ;\, - 6} \right);\,\,\left( { - \sqrt 3 ;\, - 6} \right).\)
Câu 2
Lời giải
Chọn D
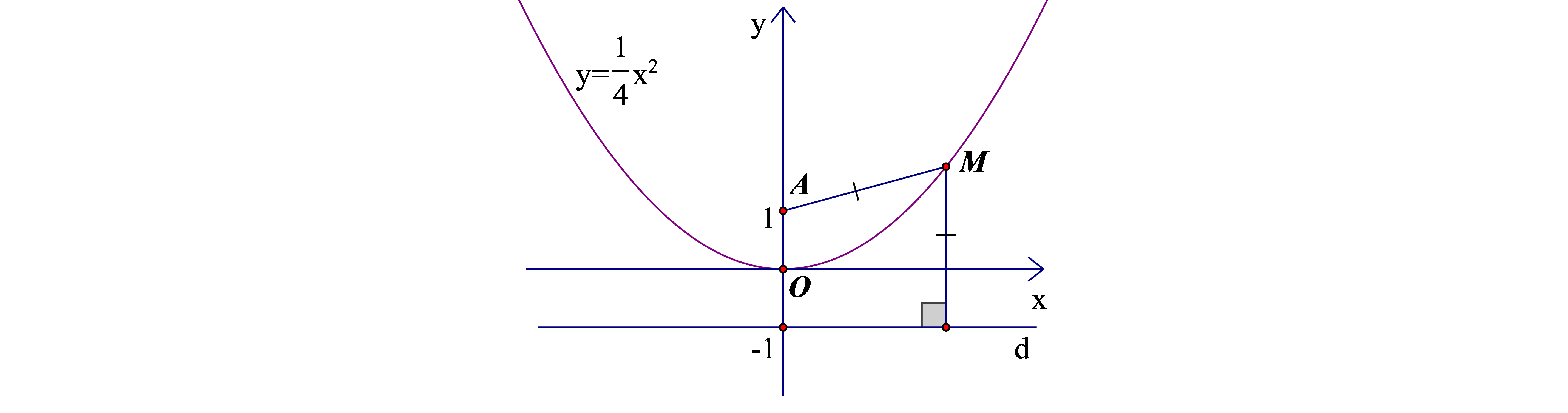
Gọi tọa độ của điểm \(M\) là \(\left( {x;y} \right)\).
Đường thẳng \(d\) đi qua điểm \(\left( {0; - 1} \right)\) và song song với trục \(Ox\)có dạng \(\left( d \right):y + 1 = 0\).
Khoảng cách từ \(M\) đến \(A\) là \(MA = \sqrt {{{\left( {0 - x} \right)}^2} + {{\left( {1 - y} \right)}^2}} \)\( = \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} \)
Khoảng cách từ \(M\) đến đường thẳng \(d\) là \(\frac{{\left| {y + 1} \right|}}{{\sqrt {{1^2}} }} = \left| {y + 1} \right|\)
Để khoảng cách từ \(M\) đến \(A\) bằng khoảng cách từ \(M\) đến đường thẳng \(d\) thì \(\sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = \left| {y + 1} \right|\)\( \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {y + 1} \right)^2}\)\( \Leftrightarrow {x^2} + {y^2} - 2y + 1 = {y^2} + 2y + 1\)\( \Leftrightarrow 4y = {x^2}\)\( \Leftrightarrow y = \frac{1}{4}{x^2}\).
Vậy tập hợp các điểm \(M\)là một parabol có phương trình \(y = \frac{1}{4}{x^2}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.