Với thiết kế độc đáo, cổng trường Đại học Bách Khoa Hà Nội được xây dựng cách đây khoảng 50 năm và đã từng là niềm tự hào của tri thức thế hệ mới. Chiếc cổng có chiều cao \(7,6\;{\rm{m}}\) và khoảng cách giữa hai chân cổng là \({\rm{AB}} = 9\;{\rm{m}}\). Một bạn sinh viên đứng cách chân cổng một đoạn \({\rm{AE}} = 0,5\;{\rm{m}}\) thì đỉnh đầu bạn ấy vừa chạm vào cổng. Hỏi bạn đó cao bao nhiêu.
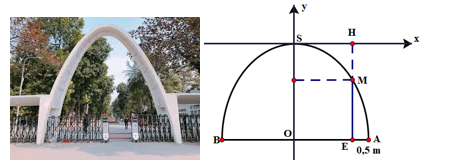
Với thiết kế độc đáo, cổng trường Đại học Bách Khoa Hà Nội được xây dựng cách đây khoảng 50 năm và đã từng là niềm tự hào của tri thức thế hệ mới. Chiếc cổng có chiều cao \(7,6\;{\rm{m}}\) và khoảng cách giữa hai chân cổng là \({\rm{AB}} = 9\;{\rm{m}}\). Một bạn sinh viên đứng cách chân cổng một đoạn \({\rm{AE}} = 0,5\;{\rm{m}}\) thì đỉnh đầu bạn ấy vừa chạm vào cổng. Hỏi bạn đó cao bao nhiêu.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương trình parabol của cổng trường có dạng: \((P):y = a{x^2}(a < 0)\).
\({\rm{OA}} = \frac{{{\rm{AB}}}}{2} = \frac{9}{2} = 4,5\;{\rm{m}};{\rm{OE}} = {\rm{OA}} - {\rm{AE}} = 4,5 - 0,5 = 4\;{\rm{m}}\). Vì \({\rm{OS}} = 7,6\;{\rm{m}} \Rightarrow {\rm{A}}(4,5; - 7,6)\).
\({\rm{A}}(4,5; - 7,6) \in (P):y = a{x^2} \Rightarrow - 7,6 = a \cdot {(4,5)^2} \Rightarrow a = \frac{{ - 7,6}}{{4,{5^2}}} = - \frac{{152}}{{405}}\)
Vậy \((P):y = - \frac{{152}}{{405}}{x^2}\)
Thay \(x = 4\) vào \((P):y = - \frac{{152}}{{405}}{x^2}\), ta có: \(y = - \frac{{152}}{{405}}{4^2} \approx - 6\)
\( \Rightarrow {\rm{HM}} = 6\;{\rm{m}} \Rightarrow {\rm{ME}} = {\rm{HE}} - {\rm{HM}} = 7,6 - 6 = 1,6\;{\rm{m}}\)
Vậy bạn sinh viên đó cao \(1,6\;{\rm{m}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
- Bảng giá trị của \[y\] tương ứng với giá trị của \[x\] như sau:
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
\[1\] |
\[2\] |
|
\[y = {x^2}\] |
\[4\] |
\[1\] |
\[0\] |
\[1\] |
\[4\] |
- Vẽ các điểm \[A\left( { - 2;4} \right),B\left( { - 1;1} \right),O\left( {0;0} \right),C\left( {1;1} \right),D\left( {2;4} \right)\] thuộc đồ thị hàm số \(y = {x^2}\) trong mặt phẳng \[Oxy\].
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số \(y = {x^2}\)
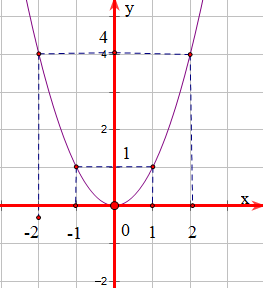
b) Gọi \(C\) là điểm thuộc \(\left( P \right)\) có tung độ bằng 16.
Ta có: \({y_C} = 16 \Leftrightarrow {x^2}_C = 16 \Leftrightarrow {x_C} = \pm 4\). Vậy \(C\left( {4;16} \right)\) hoặc \(C\left( { - 4;16} \right)\).
c) Gọi \(D\) là điểm thuộc \(\left( P \right)\) cách đều hai trục tọa độ.
Ta có: \(d\left( {D,Ox} \right) = \left| {{y_D}} \right| = x_D^2;d\left( {D,Oy} \right) = \left| {{x_D}} \right|\).
Theo giả thiết ta có: \(x_D^2 = \left| {{x_D}} \right| \Leftrightarrow \left| {{x_D}} \right| = 0\) (loại) hoặc \(\left| {{x_D}} \right| = 1\).
Vậy \(D\left( {1;1} \right)\) hoặc \(D\left( { - 1;1} \right)\).
Lời giải
a) Thay \(y = - 2\) và \(x = - 1\) vào hàm số \(y = (2m - 1){x^2}\) ta được:
\(\begin{array}{l} - 2 = (2m - 1){\left( { - 1} \right)^2}\\m = \frac{{ - 1}}{2}\end{array}\)
Vậy \(m = \frac{{ - 1}}{2}\) là giá trị cần tìm.
b) Ta đi giải các hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.\) ta được nghiệm\(\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)
Thay \(x = 2;y = 1\)và hàm số \(y = (2m - 1){x^2}\) ta có:
\(\begin{array}{l}1 = (2m - 1){.2^2}\\1 = 8m - 4\end{array}\)
\(m = \frac{5}{8}\)
Vậy \(m = \frac{5}{8}\) là giá trị cần tìm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập