Cho phương trình \({x^2} - 2x + m + 2 = 0\). Tìm m để phương trình có nghiệm \({x_1};{x_2}\) thỏa mãn điều kiện \({x_1}^2 + {x_2}^2 = 10\).
Quảng cáo
Trả lời:
Ta có: \(a = 1;b = - 2 \Rightarrow b' = - 1;c = m + 2\). Phương trình đã cho có hai nghiệm \({x_1};{x_2}\) khi và chỉ khi
\(\Delta ' \ge 0 \Leftrightarrow {\left( { - 1} \right)^2} - \left( {m + 2} \right) \ge 0 \Leftrightarrow \;m \le - 1\)
Theo hệ thức Viète, ta có: \({x_1} + {x_2} = 2;{x_1}{x_2} = m + 2\). Vậy \({x_1}^2 + {x_2}^2 = 10 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\)
\( \Leftrightarrow 4 - 2\left( {m + 2} \right) = 10 \Leftrightarrow - 2m = 10 \Leftrightarrow m = - 5{\rm{ }}\)(thỏa mãn điều kiện \(m \ge - 1\))
Đáp số: \(m = - 5\).
Cách khác: Giả sử phương trình đã cho có hai nghiệm \({x_1};{x_2}\). Theo hệ thức Viète, ta có:
\({x_1} + {x_2} = 2;{x_1}{x_2} = m + 2\) (Tương tự cách giải trên):
\({x_1}^2 + {x_2}^2 = 10 \Leftrightarrow 4 - 2\left( {\;m + 2} \right) = 10 \Leftrightarrow \;m = - 5\)
Thử lại: Với \(m = - 5\), ta có phương trình \({x^2} - 2x - 3 = 0\). Ta có \(a = 1;b = - 2;c = - 3 \Rightarrow ac = - 2 < 0 \Rightarrow \) phương trình có hai nghiệm.
Chú ý: Vì ta giả sử có nghiệm, để tìm được \(m\), sau đó ta phải thử lại. Nếu làm như cách thứ nhất, ta tìm điều kiện cho phương trình có nghiệm thì không cần thử lại.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
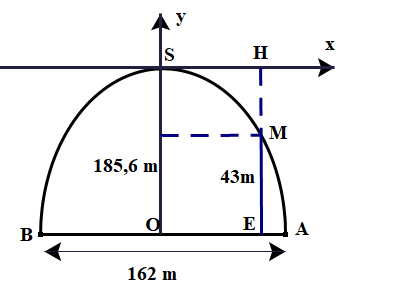
Lời giải
a) \(A\) thuộc đường thẳng \({\rm{y}} = 2{\rm{x}} - 1\) và hoành độ bằng 2 nên tung độ của \(A:y = 2.2 - 1 \Rightarrow y = 3\). Vậy \(A(2;3)\).
Lại có A là giao điểm của parabol \(y = (m + 1){x^2}\) và \(y = 2x - 1\) nên ta có \(3 = (m + 1) \cdot {(2)^2}\)
\( \Rightarrow 4\;{\rm{m}} + 4 = 3 \Rightarrow \;{\rm{m}} = - \frac{1}{4}\). Vậy \({\rm{y}} = \frac{3}{4}{{\rm{x}}^2}\).
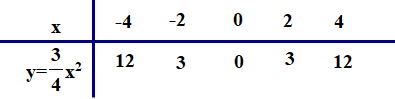
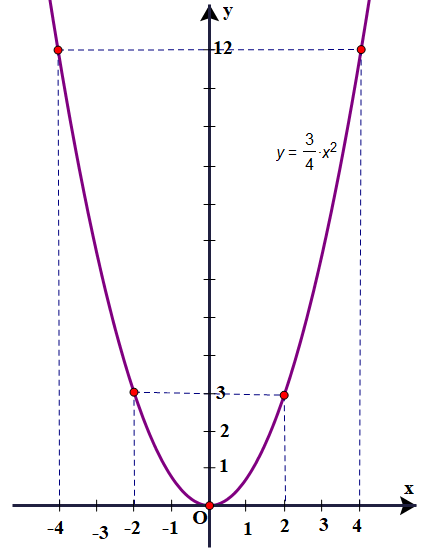
b) Vẽ parabol (P): \(y = \frac{3}{4}{x^2}\).
Bảng giá trị:
Parabol \(({\rm{P}})\) có đỉnh O và nhận trục tung làm trục đối xứng.
Lời giải
Ta có: \(a = 3;b = - 7;c = - 4 \Rightarrow a.c = - 12 < 0\). Vậy phương trình luôn có hai nghiệm phân biệt \({x_1};{x_2}\).
Theo định lí Viète, ta có: \({x_1} + {x_2} = \frac{7}{3};{x_1}{x_2} = \frac{{ - 4}}{3}\).
a) Ta có: \({A^2} = {\left| {{x_1} - {x_2}} \right|^2} = {x_1}^2 - 2{x_1}{x_2} + {x_2}^2 = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = {\left( {\frac{7}{3}} \right)^2} - 4.\left( {\frac{{ - 4}}{3}} \right) = \frac{{97}}{9} \Rightarrow A = \frac{{\sqrt {97} }}{3}\)
b) Ta có \(B = \frac{{x_1^3 + x_2^3}}{{{x_1}{x_2}}} = \frac{{{{\left( {{x_1} + {x_2}} \right)}^3} - 3{x_1}{x_2}.\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}} = \frac{{{{\left( {\frac{7}{3}} \right)}^3} - 3.\left( {\frac{{ - 4}}{3}} \right).\frac{7}{3}}}{{\frac{{ - 4}}{3}}} = - \frac{{595}}{{36}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.