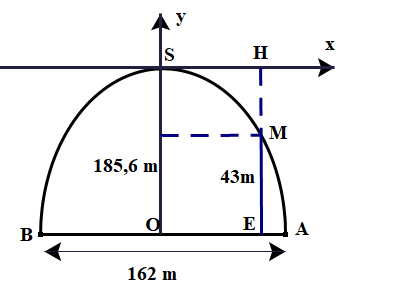
Một xe tải có chiều rộng là \(2,4\;{\rm{m}}\) chiều cao là \(2,5\;{\rm{m}}\) muốn đi qua một cái cổng hình parabol. Biết khoảng cách giữa hai chân cổng là 4 m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là \(2\sqrt 5 \;{\rm{m}}\) (bỏ qua độ dày của cổng).
a) Trong mặt phẳng tọa độ \(Oxy\) gọi parabol \((P):y = a{x^2}\) với a \( < 0\) là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh \(a = - 1\).
b) Hỏi xe tải có đi qua cổng được không? Tại sao?

Một xe tải có chiều rộng là \(2,4\;{\rm{m}}\) chiều cao là \(2,5\;{\rm{m}}\) muốn đi qua một cái cổng hình parabol. Biết khoảng cách giữa hai chân cổng là 4 m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là \(2\sqrt 5 \;{\rm{m}}\) (bỏ qua độ dày của cổng).
a) Trong mặt phẳng tọa độ \(Oxy\) gọi parabol \((P):y = a{x^2}\) với a \( < 0\) là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh \(a = - 1\).
b) Hỏi xe tải có đi qua cổng được không? Tại sao?

Quảng cáo
Trả lời:
a) Giả sử trên mặt phẳng tọa độ, độ dài các đoạn thẳng được tính theo đơn vị mét. Do khoảng cách giữa hai chân cổng là 4 m nên \({\rm{MA}} = {\rm{NA}} = 2\;{\rm{m}}\). Theo giả thiết ta có \({\rm{OM}} = {\rm{ON}} = 2\sqrt 5 \).
Xét vuông tại \(A\), ta có: \({\rm{OA}} = \sqrt {{\rm{O}}{{\rm{M}}^2} - {\rm{A}}{{\rm{M}}^2}} = \sqrt {{{(2\sqrt 5 )}^2} - {2^2}} = 4\;{\rm{m}}\).
\( \Rightarrow {\rm{M}}(2; - 4) \in (P):y = a{x^2} \Rightarrow - 4 = a{.2^2} \Rightarrow a = - 1\).
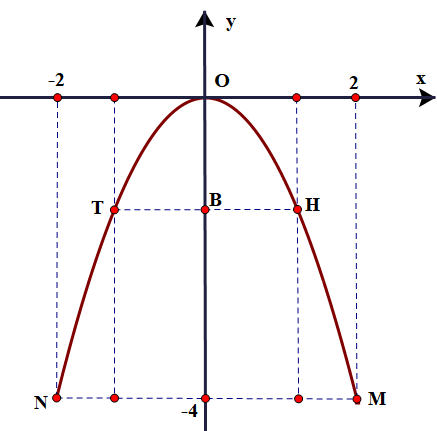
b) Để đáp ứng chiều cao trước hết xe tải phải đi vào chính giữa cổng.
\( \Rightarrow {\rm{AB}} = 2,5\;{\rm{m}} \Rightarrow {\rm{OB}} = {\rm{OA}} - {\rm{AB}} = 4 - 2,5 = 1,5\;{\rm{m}}\)
\(({\rm{HT}}):y = - \frac{3}{2}\)
Đường thẳng này cắt Parabol tại 2 điểm có tọa độ thỏa mãn hệ: \(\left\{ {\begin{array}{*{20}{l}}{y = - {x^2}}\\{y = - \frac{3}{2}}\end{array}} \right.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} = \frac{3}{2}}\\{y = - \frac{3}{2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{{3\sqrt 2 }}{2}}\\{y = - \frac{3}{2}}\end{array}} \right.} \right.\) hay \(\left\{ {\begin{array}{*{20}{l}}{x = - \frac{{3\sqrt 2 }}{2}}\\{y = - \frac{3}{2}}\end{array} \Rightarrow H\left( {\frac{{3\sqrt 2 }}{2}; - \frac{3}{2}} \right),T\left( { - \frac{{3\sqrt 2 }}{2}; - \frac{3}{2}} \right)} \right.\)
\( \Rightarrow {\rm{HT}} = 3\sqrt 2 \approx 4,24\;{\rm{m}} > 2,4\;{\rm{m}}.\)Vậy xe tải có thể đi qua cổng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) \(A\) thuộc đường thẳng \({\rm{y}} = 2{\rm{x}} - 1\) và hoành độ bằng 2 nên tung độ của \(A:y = 2.2 - 1 \Rightarrow y = 3\). Vậy \(A(2;3)\).
Lại có A là giao điểm của parabol \(y = (m + 1){x^2}\) và \(y = 2x - 1\) nên ta có \(3 = (m + 1) \cdot {(2)^2}\)
\( \Rightarrow 4\;{\rm{m}} + 4 = 3 \Rightarrow \;{\rm{m}} = - \frac{1}{4}\). Vậy \({\rm{y}} = \frac{3}{4}{{\rm{x}}^2}\).
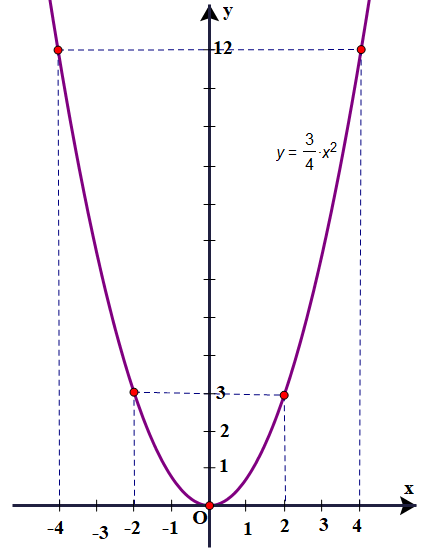
b) Vẽ parabol (P): \(y = \frac{3}{4}{x^2}\).
Bảng giá trị:
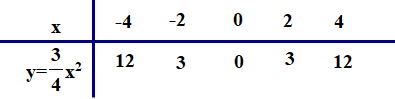
Parabol \(({\rm{P}})\) có đỉnh O và nhận trục tung làm trục đối xứng.
Lời giải
Ta có: \(a = 3;b = - 7;c = - 4 \Rightarrow a.c = - 12 < 0\). Vậy phương trình luôn có hai nghiệm phân biệt \({x_1};{x_2}\).
Theo định lí Viète, ta có: \({x_1} + {x_2} = \frac{7}{3};{x_1}{x_2} = \frac{{ - 4}}{3}\).
a) Ta có: \({A^2} = {\left| {{x_1} - {x_2}} \right|^2} = {x_1}^2 - 2{x_1}{x_2} + {x_2}^2 = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = {\left( {\frac{7}{3}} \right)^2} - 4.\left( {\frac{{ - 4}}{3}} \right) = \frac{{97}}{9} \Rightarrow A = \frac{{\sqrt {97} }}{3}\)
b) Ta có \(B = \frac{{x_1^3 + x_2^3}}{{{x_1}{x_2}}} = \frac{{{{\left( {{x_1} + {x_2}} \right)}^3} - 3{x_1}{x_2}.\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}} = \frac{{{{\left( {\frac{7}{3}} \right)}^3} - 3.\left( {\frac{{ - 4}}{3}} \right).\frac{7}{3}}}{{\frac{{ - 4}}{3}}} = - \frac{{595}}{{36}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.