Một khu vườn hình chữ nhật có chu vi \(280\;{\rm{m}}\). Người ta làm một lối đi xung quanh vườn thuộc đất của vườn rộng \(2\;{\rm{m}}\), diện tích đất còn lại để trồng trọt là \(4256\;{{\rm{m}}^2}\). Tính các kích thước của vườn.
Quảng cáo
Trả lời:
Gọi chiều dài hình chữ nhật là \(x\,(\;{\rm{m}},x > 70)\), khi đó, chiều rộng của khi vườn hình chữ nhật \(280 \div 2 - x = 140 - x(\;{\rm{m}}).\)
Người ta làm một lối đi xung quanh vườn thuộc đất của vườn rộng \(2\;{\rm{m}}\), thì chiều dài phần đất còn lại để trồng trọt là \(x - 4(\;{\rm{m}})\), chiều rộng phần đất còn lại để trồng trọt là \(140 - x - 4 = 136 - x\) \(({\rm{m}}).\)
Theo đầu Câu, diện tích đất trồng còn lại là \(4256\;{{\rm{m}}^2}\), ta có phương trình
\((x - 4) \cdot (136 - x) = 4256 \Leftrightarrow {x^2} - 140x + 4800 = 0.\)
Ta có \(\Delta = {140^2} - 4 \cdot (4800) = 400 > 0\) nên phương trình có nghiệm \({x_1} = 60\) (loại); \({x_2} = 80\) (nhận).
Vậy chiều dài mãnh đất hình chữ nhật là \(80\;{\rm{m}}\), chiều rộng là \(60\;{\rm{m}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) \(A\) thuộc đường thẳng \({\rm{y}} = 2{\rm{x}} - 1\) và hoành độ bằng 2 nên tung độ của \(A:y = 2.2 - 1 \Rightarrow y = 3\). Vậy \(A(2;3)\).
Lại có A là giao điểm của parabol \(y = (m + 1){x^2}\) và \(y = 2x - 1\) nên ta có \(3 = (m + 1) \cdot {(2)^2}\)
\( \Rightarrow 4\;{\rm{m}} + 4 = 3 \Rightarrow \;{\rm{m}} = - \frac{1}{4}\). Vậy \({\rm{y}} = \frac{3}{4}{{\rm{x}}^2}\).
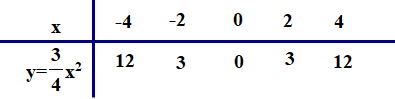
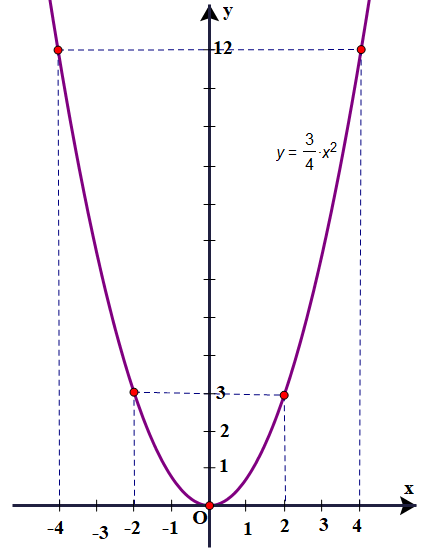
b) Vẽ parabol (P): \(y = \frac{3}{4}{x^2}\).
Bảng giá trị:
Parabol \(({\rm{P}})\) có đỉnh O và nhận trục tung làm trục đối xứng.
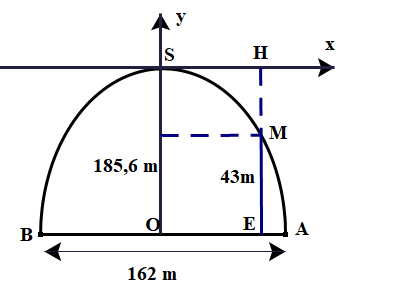
Lời giải
Ta có: \(a = 3;b = - 7;c = - 4 \Rightarrow a.c = - 12 < 0\). Vậy phương trình luôn có hai nghiệm phân biệt \({x_1};{x_2}\).
Theo định lí Viète, ta có: \({x_1} + {x_2} = \frac{7}{3};{x_1}{x_2} = \frac{{ - 4}}{3}\).
a) Ta có: \({A^2} = {\left| {{x_1} - {x_2}} \right|^2} = {x_1}^2 - 2{x_1}{x_2} + {x_2}^2 = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = {\left( {\frac{7}{3}} \right)^2} - 4.\left( {\frac{{ - 4}}{3}} \right) = \frac{{97}}{9} \Rightarrow A = \frac{{\sqrt {97} }}{3}\)
b) Ta có \(B = \frac{{x_1^3 + x_2^3}}{{{x_1}{x_2}}} = \frac{{{{\left( {{x_1} + {x_2}} \right)}^3} - 3{x_1}{x_2}.\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2}}} = \frac{{{{\left( {\frac{7}{3}} \right)}^3} - 3.\left( {\frac{{ - 4}}{3}} \right).\frac{7}{3}}}{{\frac{{ - 4}}{3}}} = - \frac{{595}}{{36}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.