Cho đường tròn tâm (O) , đường kính AB và S là một điểm nằm bên ngoài đường tròn, SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. CHứng minh rằng SH vuông góc với AB.
Cho đường tròn tâm (O) , đường kính AB và S là một điểm nằm bên ngoài đường tròn, SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. CHứng minh rằng SH vuông góc với AB.
Câu hỏi trong đề: 6 bài tập Sử dụng tính chất của góc nội tiếp (có lời giải) !!
Quảng cáo
Trả lời:
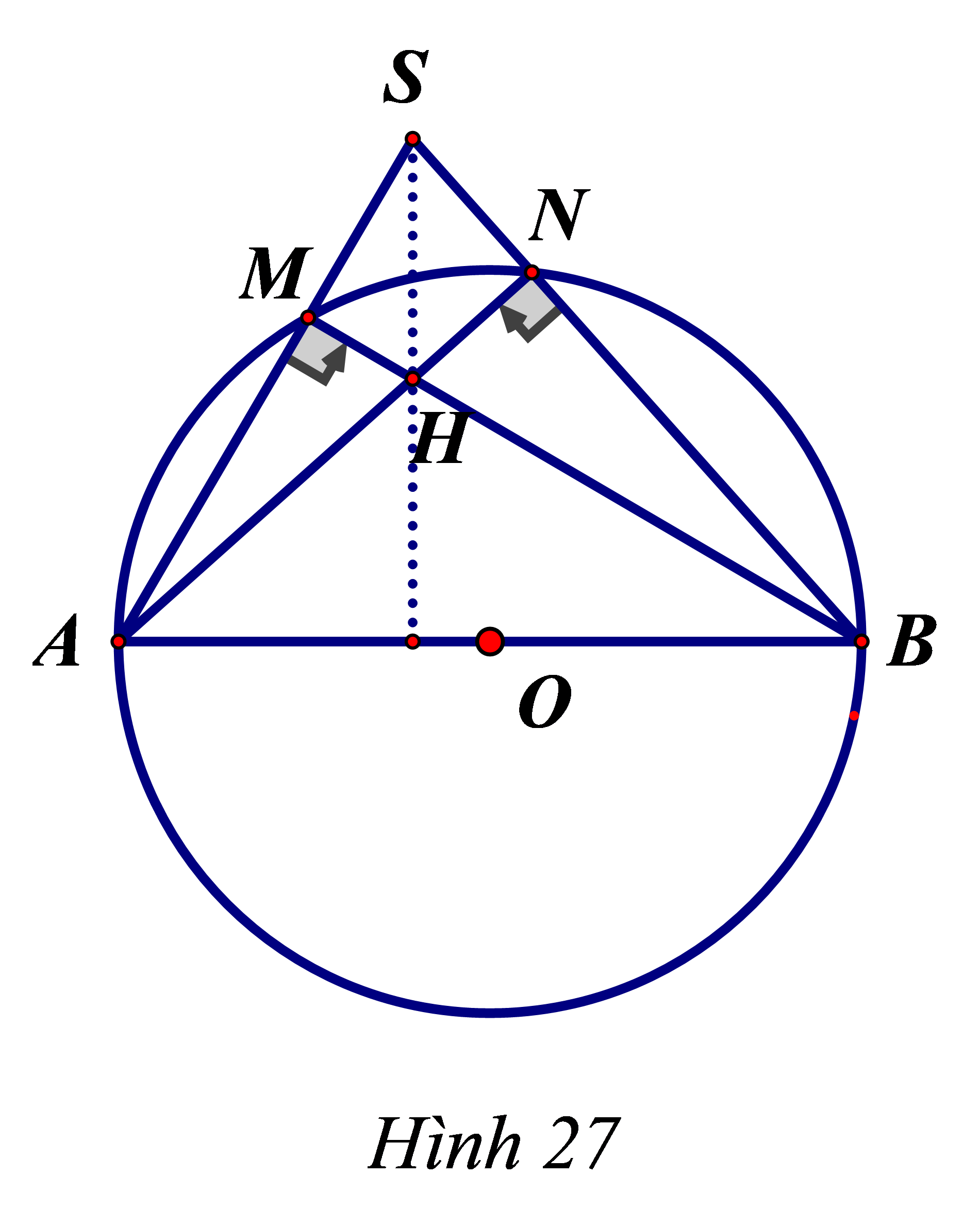
Ta có: \(\widehat {AMB} = \widehat {ANB} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn đường kính AB) .
Suy ra: AN \( \bot \)SB; BM \( \bot \)SA.
Xét ∆SAB có hai đường cao AN và BM cắt nhau tại H. Theo tính chất ba đường cao của tam giác gặp nhau tại một điểm, suy ra: SH \( \bot \) AB.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) \(\widehat {MAN} = 30^\circ \)\( \Rightarrow \widehat {MBN} = 60^\circ \Rightarrow \widehat {PCQ} = 120^\circ \)
b) \(\widehat {PCQ} = 136^\circ \) \( \Rightarrow \widehat {MBN} = 68^\circ \Rightarrow \widehat {MAN} = 34^\circ \).
Lời giải
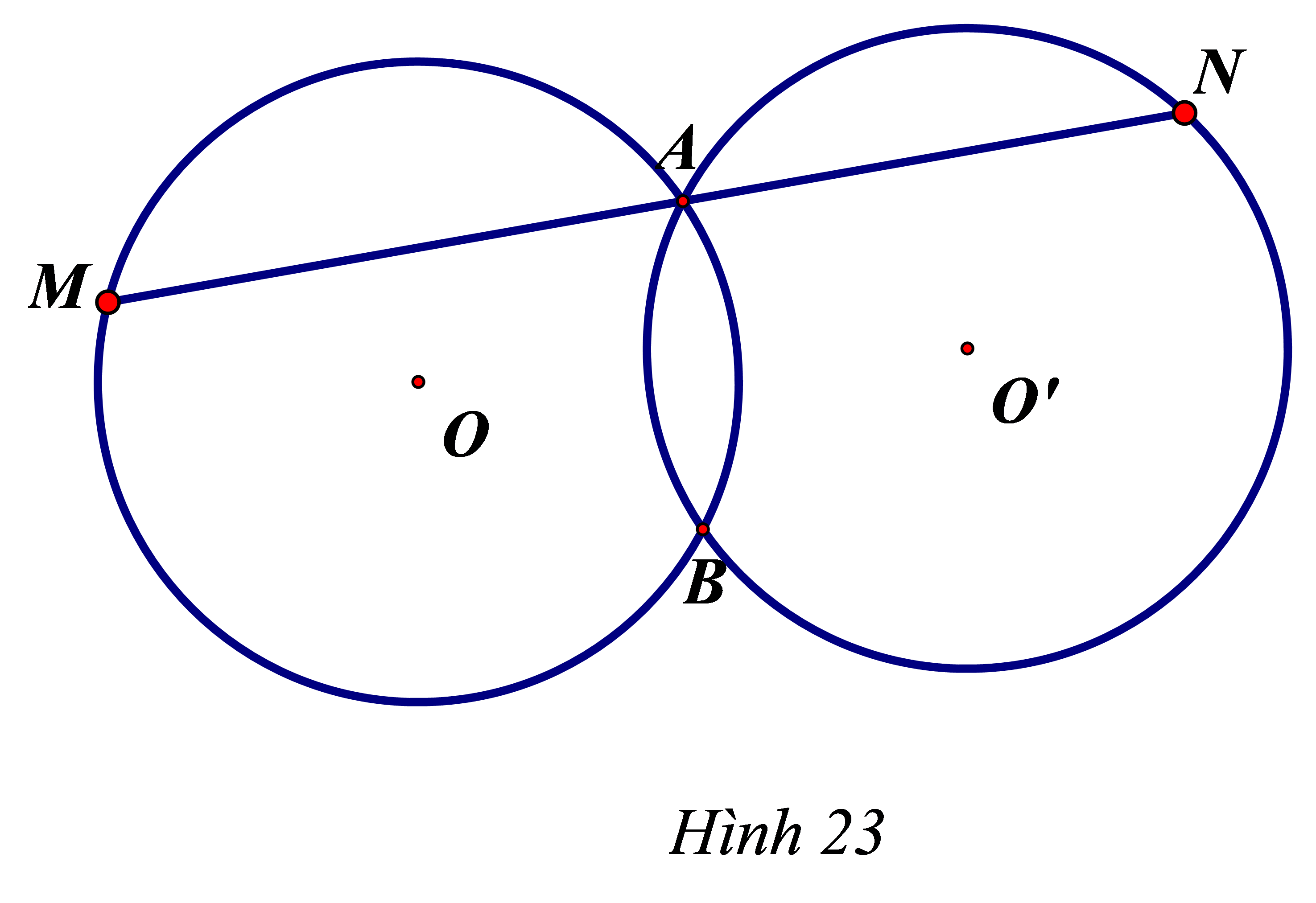
Hai đường tròn (O) và (O’) bằng nhau nên hai cung nhỏ AB bằng nhau (vì cùng căng dây AB) .
Suy ra \(\widehat M = \widehat N\)(hai góc nội tiếp chắn hai cung bằng nhau)
Vậy \(\Delta \)MBN là tam giác cân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Cho AB, BC, CA là ba dây của đường tròn (O) Tử điểm chính giữa M của cung AB vẽ dây MN song song với dây BC. Gọi giao điểm của MN và AC là S. Chứng minh SM = SC và \[SN = SA.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/screenshot-5563-1769674612.png)