Cho ngũ giác ABCDE có các cạnh bằng nhau và ˆ A = ˆ B = ˆ C = 108 ∘ Ngũ giác ABCDE có phải là ngũ giác đều không?
Quảng cáo
Trả lời:
Giải bởi Vietjack
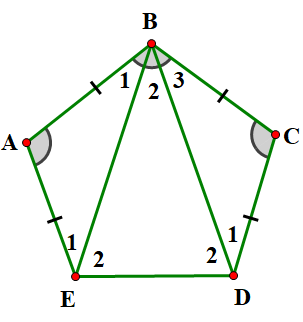
Ta có: \(AB = BC = CD = DE = EA\) (gt) (*).
Xét tam giác \(ABE\) có \({\rm{AB}} = {\rm{AE}}\) (gt) nên cân tại \(A\) có (gt)
Tương tự với tam giác BCD , ta có: \[\widehat {{B_3}} = \widehat {{D_1}}\].
Lại có
Dễ thấy \( \Rightarrow BE = BD\) hay tam giác \(EBD\) cân tại \(B\) có
. Khi đó
Tương tự . Vậy
Từ \(^{(*)}\) và \(\left( {^{(*)}} \right) \Rightarrow \) Ngũ giác \[ABCDE\]là ngũ giác đều (Các cạnh bằng nhau, các góc bằng nhau).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
Nhắn tin Zalo
Hỏi bài tập