6 bài tập Nhận dạng đa giác đều (có lời giải)
58 người thi tuần này 4.6 113 lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
Danh sách câu hỏi:
Lời giải
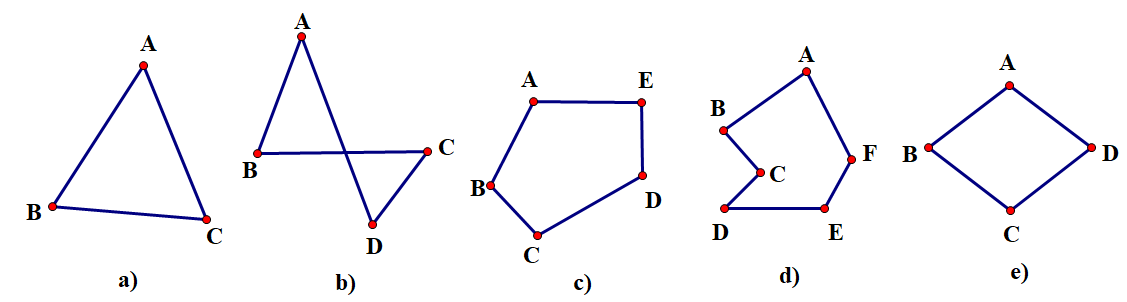
Các đa giác trong hình \({\rm{a}},{\rm{c}}\), e là các đa giác lồi vì đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác.
Đa giác ở hình \(b\) không phải là đa giác lồi vì không cùng nằm về một phía so với đường thẳng \(AD\)hoặc \(BC\).
Ở hình d cũng không phải là đa giác lồi vì không cùng nằm về một phía so với đường thẳng \(BC\) hoặc \(DC\).
Lời giải
Hình phẳng có dạng đa giác đều là hình b và d.
Lời giải
Hình 3b là ngũ giác đều, Hình 3d là hình bát giác đều; Hình 3e là tứ giác đều; Hình 3g là lục giác đều.
Lời giải
Các đa giác đều có trong hình là: Tam giác đều, tứ giác đều và lục giác đều.
Lời giải
![Cho đường tròn \[\left( {O;R} \right)\]. Lấy các điểm \(A,B,C,D,E,F\) trên đường tròn \(\left( {O;R} \right)\) sao cho số đo các cung bằng nhau. Đa giác \[ABCDEF\] có là đa giác đều không? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/2-1769708061.png)
Ta có .
Xét tam giác \(AOB\) cân tại \(O\) có (vì )
đều nên \(AB = R\) và \(\widehat {ABO} = {60^^\circ }\) (1)
Tương tự với tam giác BOC đều và \({\rm{BC}} = {\rm{R}}\) (2)
Từ (1) và (2) và \(AB = BC = R\).
Chứng minh tương tự với các cạnh và các góc còn lại ta có đa giác \(ABCD\) có:
\(AB = BC = CD = DE = EF = FA = R.\)
Và các góc \(\widehat {{\rm{ABC}}} = \widehat {{\rm{BCD}}} = \widehat {{\rm{CDE}}} = \widehat {{\rm{DEF}}} = \widehat {{\rm{EFA}}} = \widehat {{\rm{FAB}}} = 120^\circ \). Do đó \[ABCDEF\] là một đa giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.