Cho ngũ giác đều \[MNPQR\] có tâm \[O.\] Phép quay nào với tâm \[O\] biến ngũ giác đều \[MNPQR\] thành chính nó?
Quảng cáo
Trả lời:
Chọn B
![Cho ngũ giác đều \[MNPQR\] có tâm \[O.\] Phép quay nào với tâm \[O\] biến ngũ giác đều \[MNPQR\] thành chính nó? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/11-1769713058.png)
Các phép quay giữ nguyên ngũ giác đều \[MNPQR\] là:
⦁ Năm phép quay thuận chiều \[\alpha ^\circ \] tâm \[O\] với \[\alpha ^\circ \] lần lượt nhận các giá trị:
\[\alpha _1^o = \frac{{360^\circ }}{5} = 72^\circ ;\,\,\alpha _2^o = \frac{{2 \cdot 360^\circ }}{5} = 144^\circ ;\,\,\alpha _3^o = \frac{{3 \cdot 360^\circ }}{5} = 216^\circ ;\]
\[\alpha _4^o = \frac{{4 \cdot 360^\circ }}{5} = 288^\circ ;\,\,\alpha _5^o = \frac{{5 \cdot 360^\circ }}{5} = 360^\circ .\]
⦁ Ba phép quay ngược chiều \[\alpha ^\circ \] tâm \[O\] với \[\alpha ^\circ \] lần lượt nhận các giá trị:
\[\alpha _1^o = \frac{{360^\circ }}{5} = 72^\circ ;\,\,\alpha _2^o = \frac{{2 \cdot 360^\circ }}{5} = 144^\circ ;\,\,\alpha _3^o = \frac{{3 \cdot 360^\circ }}{5} = 216^\circ ;\]
\[\alpha _4^o = \frac{{4 \cdot 360^\circ }}{5} = 288^\circ ;\,\,\alpha _5^o = \frac{{5 \cdot 360^\circ }}{5} = 360^\circ .\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn C
![Góc \[BAD\] và \[BOD\] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/7-1769712875.png)
Góc \[ACM\] là góc nội tiếp chắn nửa đường tròn \[\left( O \right)\] nên \(\widehat {ACM} = 90^\circ \).
Xét hai tam giác \(ABH\) và \[AMC\] có:
\(\widehat {AHB} = \widehat {ACM} = 90^\circ \)
\(\widehat {ABH} = \widehat {AMC}\) (hai góc nội tiếp cùng chắn cung \[AC\] của \[\left( O \right)\])
Nên (g.g)
Suy ra \(\widehat {BAH} = \widehat {OAC};\widehat {OCA} = \widehat {OAC}\).
Do đó \(\widehat {BAH} = \widehat {OCA}\).
Góc \[ANM\] là góc nội tiếp chắn nửa đường tròn \[\left( O \right)\] nên \(\widehat {ANM} = 90^\circ \).
Suy ra \[MNBC\] là hình thang, suy ra \[BC\,{\rm{//}}\,MN\] và \(\widehat {CBN} = \widehat {BCM}\).
Vậy \[BCMN\] là hình thang cân.
Câu 2
Lời giải
Chọn B
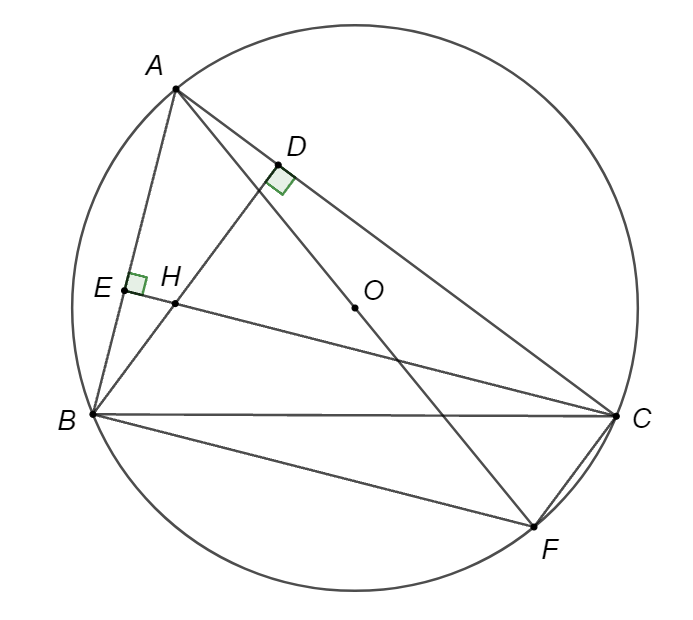
Tam giác \(BEH\) vuông tại \(E\) nên \(BH > BE\). Do đó khẳng định A sai.
Xét \[\left( O \right)\] có \(\widehat {ACF} = 90^\circ \); \(\widehat {ABF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Suy ra \[CF \bot AC;{\rm{ }}BF\; \bot \;AB\] mà \[BD\; \bot \;AC;{\rm{ }}CE\; \bot \;AB\]
Suy ra \[BD\,{\rm{//}}\,CF;{\rm{ }}CE\,{\rm{//}}\,BF\].
Do đó \[BHCF\] là hình bình hành.
Suy ra \[BH = CF\]. Do đó khẳng định B đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Tứ giác \[ABCD\] nội tiếp (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/10-1769712984.png)