Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(A\left( {0;0;0} \right);B\left( {3;0;0} \right);D\left( {0;2;0} \right);A'\left( {0;0;5} \right)\).

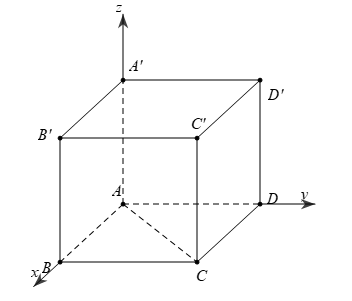
a)Đúng

Hình chiếu của điểm \(C\) trên các trục \(Ox,Oy,Oz\) lần lượt là \(B,D,A\) nên \(C\left( {3;2;0} \right)\).

b) Sai

Ta có \(AB = 3;AD = 2;AA' = 5\).

\({V_{ABCD.A'B'C'D'}} = AB.AD.AA' = 2.3.5 = 30\).

c) Sai

Phương trình mặt phẳng \(\left( {A'BD} \right)\) là: \(\frac{x}{3} + \frac{y}{2} + \frac{z}{5} = 1 \Leftrightarrow 10x + 15y + 6z - 30 = 0\).

\(d\left( {A;\left( {A'BD} \right)} \right) = \frac{{\left| { - 30} \right|}}{{\sqrt {{{10}^2} + {{15}^2} + {6^2}} }} = \frac{{30}}{{19}}\).

d) Đúng

\(B'\left( {3;0;5} \right);D'\left( {0;2;5} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB'}  = \left( {3;0;5} \right)\\\overrightarrow {AD'}  = \left( {0;2;5} \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {AB'} ,\overrightarrow {AD'} } \right] = \left( { - 10; - 15;6} \right)\).

Vậy mặt phẳng \(\left( {AB'D'} \right)\) có 1 VTPT \(\overrightarrow n \left( {10;15; - 6} \right)\).

\(C\left( {3;2;0} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {B'C}  = \left( {0;2; - 5} \right)\\\overrightarrow {D'C}  = \left( {3;0; - 5} \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {B'C} ,\overrightarrow {D'C} } \right] = \left( { - 10; - 15; - 6} \right)\).

Vậy mặt phẳng \(\left( {CB'D'} \right)\) có 1 VTPT \(\overrightarrow {n'} \left( {10;15;6} \right)\).