Cho hàm số \[y = \frac{1}{3}{x^3}--2m{x^2} + \left( {m + 3} \right)x--5 + m\]. Tìm \(m\)để \(y' \ge 0,\forall x \in \mathbb{R}\)
Câu hỏi trong đề: Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có:
\(\begin{array}{l}y' = {x^2} - 4mx + m + 3\\y' \ge 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' \le 0\\1 > 0\end{array} \right. \Leftrightarrow 4{m^2} - m - 3 \le 0 \Leftrightarrow \frac{{ - 3}}{4} \le m \le 1\end{array}\)Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[30;\;22\] triệu đồng.
B. \[20;\;39\] triệu đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Điều kiện: \(x > 0,x \in \mathbb{N}\).
Doanh nhiệp thu được lợi nhuận là:
\(P\left( x \right) = R\left( x \right) - C\left( x \right)\)\( = \left( {4000x - 33{x^2}} \right) - \left( {2{x^3} - 3{x^2} + 400x + 5000} \right)\) \( = - 2{x^3} - 30{x^2} + 3600x - 5000\)
Lợi nhuận biên là: \[P'\left( x \right) = - 6{x^2} - 60x + 3600\].
Lợi nhuận tối đa đạt được tại một trong các điểm \({x_0}\) mà \[P'\left( {{x_0}} \right) = 0\].
\[P'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 30\;(loai)\\x = 20\;\;(Thoa\;man)\end{array} \right.\]
Ta có bảng xét dấu của \[P'\left( x \right)\]:
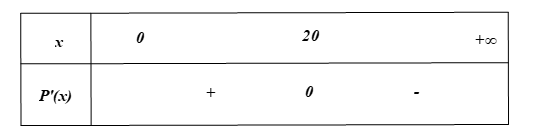
Từ bảng xét dấu của \[P'\left( x \right)\] ta có:
Khi \(x < 20\) thì \[P'\left( x \right) > 0\] nên nếu tiếp tục sản xuất thì lợi nhuận tăng.
Khi \(x > 20\) thì \[P'\left( x \right) > 0\] nên nếu tiếp tục sản xuất thì lợi nhuận giảm.
Vậy mức sản lượng tối ưu là \(20\).
Doanh thu lúc đó là: \(P\left( {20} \right) = 39000\) nghìn đồng hay \(39\) triệu đồng.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đạo hàm của hàm số \(f\) biểu thị tốc độ tăng dân số của thành phố đó (tính bằng nghìn người/ năm), ta có: \({f^\prime }(t) = \frac{{120}}{{{{(t + 5)}^2}}}\).
Từ năm 2015 đến năm 2025 nghĩa là \(t = 10\).
Vậy tốc độ tăng dân số tại thời điểm \(t = 10\) là:
\({f^\prime }(10) = \frac{{120}}{{{{(10 + 5)}^2}}} = \frac{8}{{15}} \approx 0,533{\rm{ }}\)(nghìn người/năm)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) \(y'\left( 0 \right) = 7\)
b) Đồ thị của hàm số \(y'\) đi qua điểm \(A\left( {1;\frac{7}{3}} \right)\)
c) \(y'\left( 1 \right) < y'\left( 2 \right)\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập