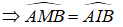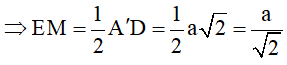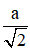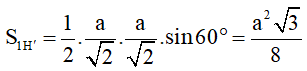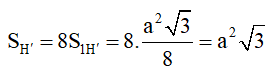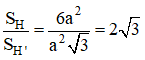Câu hỏi:

13/07/2024 2,060

Cho mặt cầu (O; R) tiếp xúc với mặt phẳng (P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với I qua tâm O. Từ M ta kẻ hai tiếp tuyến của mặt cầu cắt (P) tại A và B. Chứng minh rằng góc (AMB)= góc (AIB)

Xem lời giải

Câu hỏi trong đề: Giải bài tập Hình học 12 !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Giải bài 6 trang 49 sgk Hình học 12 | Để học tốt Toán 12

* Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA

Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.

Ta có AM và AI là hai tiếp tuyến cắt nhau tại A của mặt cầu nên:

AM = AI ( tính chất hai tiếp tuyến cắt nhau)

* Tương tự có BM = BI.

* Xét hai tam giác AMB và tam giác AIB có:

AM = AI

BM = BI

AB chung

Suy ra: ∆ AMB = ∆ AIB ( c.c.c)

Giải bài 6 trang 49 sgk Hình học 12 | Để học tốt Toán 12

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình lập phương (H). Gọi (H’) là hình bát diện đều có các đỉnh là tâm các mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H’).

Xem đáp án

Lời giải

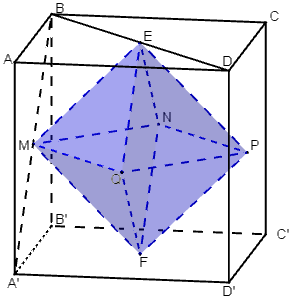
Giải bài tập Toán 12 | Để học tốt Toán 12

Gọi a là cạnh của hình lập phương ABCD.A1B1C1D1;

⇒ Diện tích toàn phần của hình lập phương (H) là: SH = 6.a2 (đvdt).

Gọi tâm các mặt lần lượt là E, F, M, N, P, Q như hình vẽ.

⇒ (H’) là bát diện đều EMNPQF.

+ Áp dụng định lí pytago vào tam giác vuông AA’D ⇒ A’D = a√2

+ EM là đường trung bình của ΔBA’D

QUẢNG CÁO

Giải bài tập Toán 12 | Để học tốt Toán 12

⇒ (H’) là bát diện đều gồm 8 mặt là các tam giác đều cạnh bằng Giải bài tập Toán 12 | Để học tốt Toán 12

⇒ Diện tích một mặt của (H’) là:

Giải bài tập Toán 12 | Để học tốt Toán 12

⇒ Diện tích toàn phần của (H’) là:

Giải bài tập Toán 12 | Để học tốt Toán 12

Vậy tỉ số diện tích cần tính là:

Giải bài tập Toán 12 | Để học tốt Toán 12

Câu 2

Từ một điểm M nằm ngoài mặt cầu (O; R), vẽ hai đường thẳng cắt mặt cầu lần lượt tại A, B và C, D.
Chứng minh rằng MA.MB = MC.MD

Xem đáp án

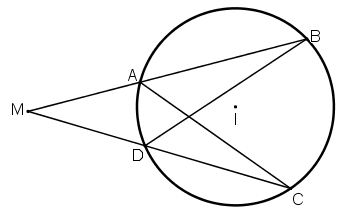
Lời giải

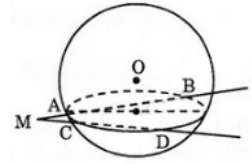
Giải bài 5 trang 49 sgk Hình học 12 | Để học tốt Toán 12

Hai đường thẳng MAB và MCD giao nhau xác định một mặt phẳng (P). Mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn (C), ngoại tiếp tứ giác phẳng ABCD.

Giải bài 5 trang 49 sgk Hình học 12 | Để học tốt Toán 12

Xét ΔMAC và ΔMDB có:

Giải bài 5 trang 49 sgk Hình học 12 | Để học tốt Toán 12

⇒ MA.MB = MC.MD (đpcm).

Câu 3