Câu hỏi:
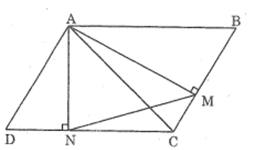
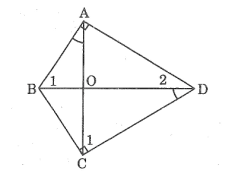
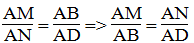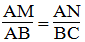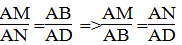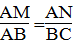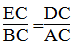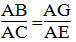13/07/2024 11,896Cho hình bình hành ABCD .Từ A kẻ AM vuông góc với BC,AN vuông góc CD (M thuộc BC và N thuộc CD). Chứng mình rằng tam giác MAN đồng dạng với tam giác ABC.
Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
* Trường hợp góc B nhọn:
Xét AMB và AND, ta có:
(AMB) = (AND) =
B = D (t/chất hình bình hành) ⇒ AMB đồng dạng AND (g.g)
Suy ra: 
Mà AD = BC (t/chất hình hình hành)
Suy ra: 
Lại có: AB // CD (gt)
AN ⊥ CD (gt)
Suy ra: AN ⊥ AB hay (NAB) =
suy ra: NAM + MAB = (1)
Trong tam giác vuông AMB ta có ABM =
Suy ra: (MAB) + B = (2)
Từ (1) và (2) suy ra: NAM = B
Xét ABC và MAN ta có:
(chứng minh trên)
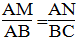
(NAM) = B (chứng minh trên)
Vậy ABC đồng dạng MAN (c.g.c)
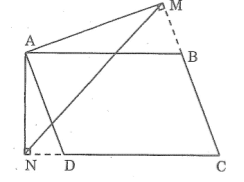
* Trường hợp góc B tù:
Xét MAN và AND, ta có:
(AMB) = (AND) =
(ABM) = (ADN) (vì cùng bằng C)
⇒AMB đông dạng AND (g.g)
Suy ra:
Mà AD = BC (t/chẩt hình bình hành)
Suy ra: 
Vì AB //CD nên (ABC) + C = (3)
Tứ giác AMCN có (AMC) = (AND) =
Suy ra: (MAN) + C = (4)
Từ (3) và (4) suy ra: (MAN) = (ABC)
Xét AMN và ABC, ta có:
(chứng minh trên)
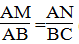
(MAN) = (ABC) (chứng minh trên)
Vậy MAN đồng dạng ABC (c.g.c)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
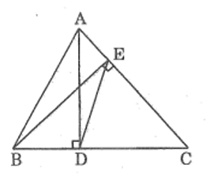
Xét ADC và BEC, ta có:
(ADC) =(BEC) =
C chung
Suy ra: ADC đồng dạng BEC (g.g)
Suy ra: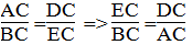
⇒ ECBC = DCAC
Xét DEC và ABC ta có:
C chung
Vậy DEC đồng dạng ABC (c.g.c)
Lời giải
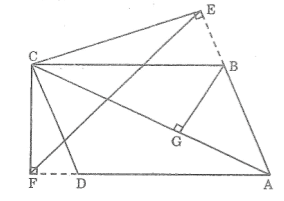
Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
(BGA) = (CEA) =
A chung
⇒BGA đồng dạng CEA(g.g)
Suy ra: 
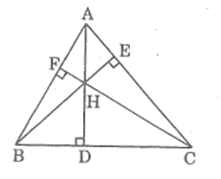
AB.AE = AC.AG (1)
Xét BGC và CFA, ta có:
(BGC) = (CFA) =
(BCG) = (CAF) (so le trong vì AD //BC)
BGC đồng dạng CFA (g.g)
Suy ra: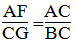 
⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
AB.AE + AD.AF= AC(AG + CG)
Mà AG + CG = AC nên AB.AE + AD.AF =
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án