Câu hỏi:
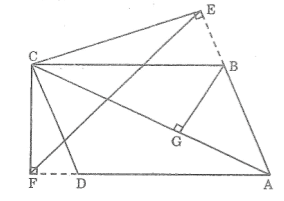
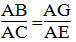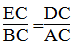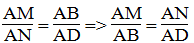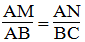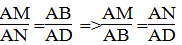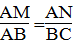13/07/2024 10,297Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD), Chứng minh rằng AB.AE + AD.AF =
Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
(BGA) = (CEA) =
A chung
⇒BGA đồng dạng CEA(g.g)
Suy ra: 
AB.AE = AC.AG (1)
Xét BGC và CFA, ta có:
(BGC) = (CFA) =
(BCG) = (CAF) (so le trong vì AD //BC)
BGC đồng dạng CFA (g.g)
Suy ra: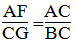 
⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
AB.AE + AD.AF= AC(AG + CG)
Mà AG + CG = AC nên AB.AE + AD.AF =
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
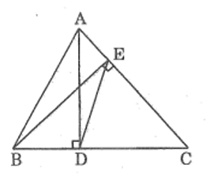
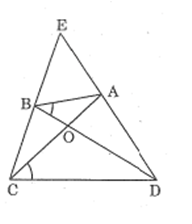
Xét ADC và BEC, ta có:
(ADC) =(BEC) =
C chung
Suy ra: ADC đồng dạng BEC (g.g)
Suy ra: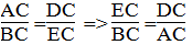
⇒ ECBC = DCAC
Xét DEC và ABC ta có:
C chung
Vậy DEC đồng dạng ABC (c.g.c)
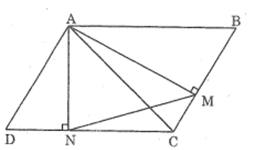
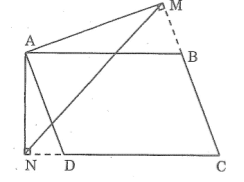
Lời giải
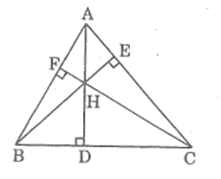
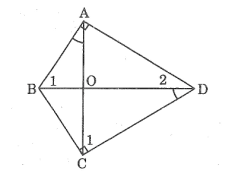
* Trường hợp góc B nhọn:
Xét AMB và AND, ta có:
(AMB) = (AND) =
B = D (t/chất hình bình hành) ⇒ AMB đồng dạng AND (g.g)
Suy ra: 
Mà AD = BC (t/chất hình hình hành)
Suy ra: 
Lại có: AB // CD (gt)
AN ⊥ CD (gt)
Suy ra: AN ⊥ AB hay (NAB) =
suy ra: NAM + MAB = (1)
Trong tam giác vuông AMB ta có ABM =
Suy ra: (MAB) + B = (2)
Từ (1) và (2) suy ra: NAM = B
Xét ABC và MAN ta có:
(chứng minh trên)
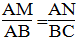
(NAM) = B (chứng minh trên)
Vậy ABC đồng dạng MAN (c.g.c)
* Trường hợp góc B tù:
Xét MAN và AND, ta có:
(AMB) = (AND) =
(ABM) = (ADN) (vì cùng bằng C)
⇒AMB đông dạng AND (g.g)
Suy ra:
Mà AD = BC (t/chẩt hình bình hành)
Suy ra: 
Vì AB //CD nên (ABC) + C = (3)
Tứ giác AMCN có (AMC) = (AND) =
Suy ra: (MAN) + C = (4)
Từ (3) và (4) suy ra: (MAN) = (ABC)
Xét AMN và ABC, ta có:
(chứng minh trên)
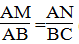
(MAN) = (ABC) (chứng minh trên)
Vậy MAN đồng dạng ABC (c.g.c)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án