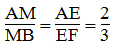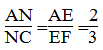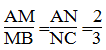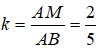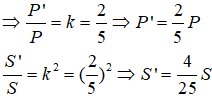Ôn tập chương 3
33 người thi tuần này 4.6 54.4 K lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
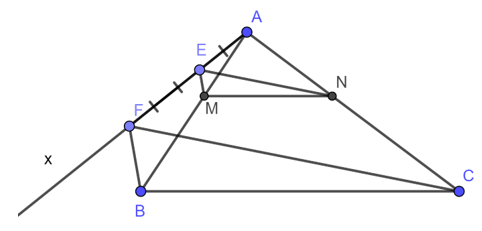
* Cách vẽ:
- Kẻ tỉa Ax bất kì khác tia AB, AC
- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)
- Kẻ đường thẳng FB
- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.
- Kẻ đường thẳng FC.
- Từ E kẻ đường thẳng song song với FC cắt AC tại N.
Ta có M, N là hai điểm cần vẽ.
* Chứng minh:
Trong ΔAFB, ta có: EM // FB.
Theo định lí Ta-lét, ta có:
Trong ΔAFC, ta có: EN // FC.
Theo định lí ta-lét ta có:
Vậy M, N là hai điểm cần tìm.
Lời giải
* Cách vẽ:
- Kẻ tỉa Ax bất kì khác tia AB, AC
- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)
- Kẻ đường thẳng FB
- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.
- Kẻ đường thẳng FC.
- Từ E kẻ đường thẳng song song với FC cắt AC tại N.
Ta có M, N là hai điểm cần vẽ.
* Chứng minh:
Trong ABC, ta có:
Suy ra: MN // BC (Theo định lí đảo của định lí Ta-lét)
Lời giải
* Cách vẽ:
- Kẻ tỉa Ax bất kì khác tia AB, AC
- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)
- Kẻ đường thẳng FB
- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.
- Kẻ đường thẳng FC.
- Từ E kẻ đường thẳng song song với FC cắt AC tại N.
Ta có M, N là hai điểm cần vẽ.
* Chứng minh:
Gọi p' và S' là chu vi và diện tích của AMN.
Trong ABC, ta có: MN // BC
Suy ra: AMN đồng dạng ΔABC
Lời giải
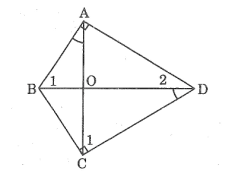
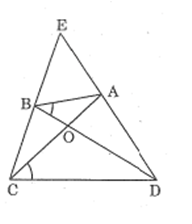
Xét ABO và DCO,ta có:
(BAO) = (BDC) (gt)
Hay (BAO) = (ODC)
(AOB) = (DOC) (đối đỉnh)
Vậy ABO đồng dạng DCO (g.g)
Lời giải
Vì ABO đồng dạng DCO nên:
(1)
Mà = (BCD) = (2)
Trong ABD, ta có: A =
Suy ra: = (3)
Từ (1), (2) và (3): Suy ra:
Xét BCO và ADO, ta có:
(chứng minh trên)
(BOC) = (AOD) (đối đỉnh)
Vậy BOC đồng dạng ADO (g.g).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.