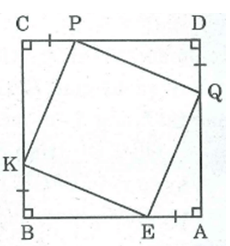
Cho hình vuông ABCD. Trên AB, BC, CD, DA lấy theo thứ tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì? Vì sao?
Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: AB = BC = CD = DA (gt)
AE = BK = CP = DQ (gt)
Suy ra: EB = KC = PD = QA
* Xét ΔAEQ và ΔBKE,ta có:
AE = BK (gt)
(EAQ) = (KBE) =
QA = EB (chứng minh trên)
Suy ra: AEQ = BKE (c.g.c) ⇒ EQ = EK (1)
* Xét BKEvà CPK,ta có: BK = CP (gt)
(KBE) = (PCK) =
EB = KC ( chứng minh trên)
Suy ra: BKE = CPK (c.g.c) ⇒ EK = KP (2)
* Xét CPK và DQP,ta có: CP = DQ (gt)
C = D =
DP = CK ( chứng minh trên)
Suy ra: CPK = DQP (c.g.c) ⇒ KP = PQ (3)
Từ (1), (2) và (3) suy ra: EK = KP = PQ = EQ
Hay tứ giác EKPQ là hình thoi.
Mặt khác: AEQ = BKE
⇒ (AQE) = (BEK)
Mà (AQE) + (AEQ) =
⇒ (BEK) + (AEQ) =
Ta có: (BEK) + (QEK) + (AEQ ) =
Suy ra: (QEK ) = -( (BEK ) + (AEQ) )= - =
Vậy tứ giác EKPQ là hình vuông.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
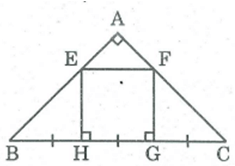
Vì ΔABC vuông cân tại A nên B = C =
Vì ΔBHE vuông tại H có B = nên ΔBHE vuông cân tại H.
Suy ra HB = HE
Vì ΔCGF vuông tại G, có C = nên ΔCGF vuông cân tại G
Suy ra GC = GF
Ta có: BH = HG = GC (gt)
Suy ra: HE = HG = GF
Vì EH // GF (hai đường thẳng cũng vuông góc với đường thắng thứ ba) nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau);
Lại có (EHG) = nên HEFG là hình chữ nhật.
Mà EH = HG (chứng minh trên).
Vậy HEFG là hình vuông.
Lời giải
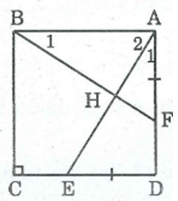
Xét ABF và DAE,ta có: AB = DA (gt)
(BAF) = (ADE) =
AF = DE (gt)
Suy ra: ΔABF = ΔDAE (c.g.c)
⇒ BF = AE và =
Gọi H là giao điểm của AE và BF.
Ta có: (BAF) = + =
Suy ra: + =
Trong ΔABH,ta có: (AHB) + + =
⇒ ((AHB) ) = – (+ ) = – =
Vậy AE ⊥ BF
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo