Câu hỏi:

13/07/2024 3,037

Chứng minh rằng ba điểm C, B, D ở hình dưới thẳng hàng.

Xem lời giải

Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 1 !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

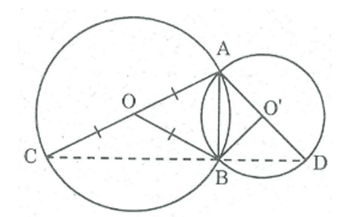
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Nối AB, BO, BC, BO', BD.

* Trong $∆$ ABC, ta có: OA = OC = R (bán kính đường tròn (O))

Nên BO là đường trung tuyến của $∆$ ABC.

Mà BO = R (bán kính (O)) ⇒ BO = OA= OC = 1/2 AC

Suy ra tam giác ABC vuông tại B ⇒ $∠$ (ABC) = $90^{0}$

* Trong $∆$ ABD , ta có: AO' = O'D = R' (bán kính đường tròn (O'))

Nên BO' là đường trung tuyến của tam giác ABD.

Mà BO' = R' (bán kính (O')) ⇒ BO' = AO' = O'D = 1/2 AD

Suy ra tam giác ABD vuông tại B ⇒ $∠$ (ABD) = $90^{0}$

Ta có: $∠$ (ABC) + $∠$ (ABD) = $∠$ (CBD) = $90^{0}$ + $90^{0}$ = $180^{0}$

Vậy C, B, D thẳng hàng.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng minh rằng AM vuông góc với DE.

Xem đáp án

Lời giải

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Xét tứ giác ADHE, ta có:

$∠$ A = $90^{0}$ (gt)

$∠$ (ADH) = $90^{0}$ (vì HD ⊥ AB)

$∠$ (AEH) = $90^{0}$ (vì HE ⊥ AC)

Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông).

+ Xét $∆$ ADH và $∆$ EHD có :

DH chung

AD = EH ( vì ADHE là hình chữ nhật)

$∠$ (ADN) = $∠$ (EHD) = $90^{0}$

Suy ra: $∆$ ADH = $∆$ EHD (c.g.c)

⇒ $∠$ $A_{1}$ = $∠$ (HED)

Lại có: $∠$ (HED) + $∠$ $E_{1}$ = $∠$ (HEA) = $90^{0}$

Suy ra: $∠$ $E_{1}$ + $∠$ $A_{1}$ = $90^{0}$

$∠$ $A_{1}$ = ∠ $A_{2}$ (chứng minh trên) ⇒ $∠$ $E_{1}$ + $∠$ $A_{2}$ = $90^{0}$

Gọi I là giao điểm của AM và DE.

Trong $∆$ AIE ta có: $∠$ (AIE) = 180o – ( $∠$ $E_{1}$ + $∠$ $A_{2}$ ) = $180^{0}$ - $90^{0}$ = $90^{0}$

Vậy AM ⊥ DE.

Câu 2

Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Tính số đo góc IHK.

Xem đáp án

Lời giải

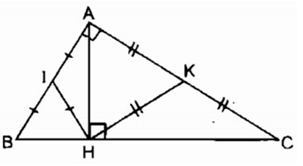
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

ΔAHB vuông tại H có HI là đường trung tuyến thuộc cạnh huyền AB

⇒ HI = IA = 1/2 AB (tính chất tam giác vuông)

⇒ $∆$ AHI cân tại I

⇒ $∠$ (IAH) = $∠$ (IHA) (1)

$∆$ AHC vuông tại H có HK là đường trung tuyến thuộc cạnh huyền AC

⇒ HK = KA = 1/2 AC (tính chất tam giác vuông)

⇒ $∆$ KAH cân tại K ⇒ $∠$ (KAH) = $∠$ (KHA) (2)

$∠$ (IHK) = $∠$ (IHA) + $∠$ (KHA) (3)

Từ (1), (2) và (3) suy ra: $∠$ (IHK) = $∠$ (IAH) + $∠$ (KAH) = $∠$ (IAK) = $∠$ (BAC) = $90^{0}$

Câu 3