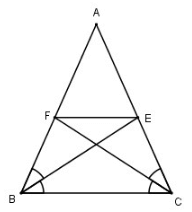
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 1 !!
Quảng cáo
Trả lời:
+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:
Mà tam giác ABC cân tại A nên B = C
Suy ra: ABE = ACF
Xét hai tam giác AEB và AFC
Có AB = AC (ABC cân tại A)
ABE = ACF (chứng minh trên)
A là góc chung
⇒ AEB = AFC (g.c.g) ⇒ AE = AF ⇒ AEF cân tại A
⇒ AFE = (− A) / 2 và trong tam giác ABC: B = (− ∠A) / 2
⇒AFE = B ⇒ FE//BC ( có hai góc ở vị trí đồng vị bằng nhau).
⇒ Tứ giác BFEC là hình thang.
Vì FE//BC nên ta có: FEB = EBC (so le trong)
Lại có: FBE = EBC ( vì BE là tia phân giác của góc B)
⇒FBE = FEB
⇒ FBE cân ở F ⇒ FB = FE
⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hai tam giác vuông AHD và BKC:
(AHD) = (BKC) =
AD = BC (tính chất hình thang cân)
C = D (gt)
Suy ra: AHD = BKC (cạnh huyền, góc nhọn)
⇒ HD = KC
Lời giải
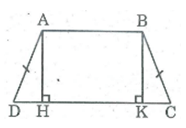
Xét ADC và BCD, ta có:
AD = BC (tính chất hình thang cân)
(ADC) = (BCD) (gt)
DC chung
Do đó: ADC = BCD (c.g.c) ⇒ =
Trong OCD ta có: = ⇒ OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
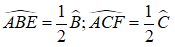
NGỌC YẾN
BE và CF lần lượt vuông góc với AC và AB (E thuộc AC ;F thuộc AB) chứng minh BF=EC
Giúp với ạ^^