Câu hỏi:

29/04/2020 3,951

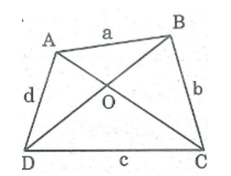
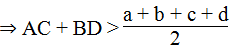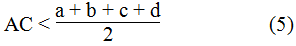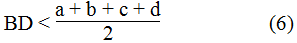Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác đó.

Xem lời giải

Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 1 !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Đặt độ dài a = AB, b = BC, c = CD, d = AD

Gọi O là giao điểm 2 đường chéo AC và BD.

* Trong $∆$ OAB, ta có:

OA + OB > a (bất đẳng thức tam giác) (1)

* Trong $∆$ OCD, ta có:

OC + OD > c (bất đẳng thức tam giác) (2)

Từ (1) và (2) suy ra:

OA + OB + OC + OD > a + c hay AC + BD > a + c (*)

* Trong $∆$ ΔOAD, ta có: OA + OD > d (bất đẳng thức tam giác) (3)

* Trong $∆$ OBC, ta có: OB + OC > b (bất đẳng thức tam giác) (4)

Từ (3) và (4) suy ra:

OA + OB + OC + OD > b + d hay AC + BD > b + d (**)

Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

* Trong $∆$ ABC, ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)

* Trong $∆$ ADC, ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)

Suy ra: 2AC < a + b + c + d

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

* Trong $∆$ ABD, ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)

* Trong $∆$ BCD, ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)

Suy ra: 2BD < a + b + c + d

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Từ (5) và (6) suy ra: AC + BD < a + b + c + d

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tứ giác ABCD có $∠$ C = $60 °$ , $∠$ D = $80 °$ , $∠$ A - $∠$ B = $10 °$ . Tính số đo các góc A và B.

Xem đáp án

Lời giải

Tổng bốn góc của 1 tứ giác bằng $360 °$ nên: ∠A + $∠$ B + $∠$ C + $∠$ D = $360 °$

Suy ra: $∠$ A + $∠$ B = $360 °$ – ( $∠$ C + $∠$ D) hay

$∠$ A + $∠$ B = $360 ° - (60 ° + 80 °) = 220 °$

Mà $∠$ A - $∠$ B = $10 °$

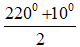
Vậy $∠$ A = Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8 = $115 °$ , $∠$ B = $115 °$ - $10 °$ = $105 °$

Câu 2

Tính tổng các góc ngoài của tứ giác (tai mỗi đỉnh của tứ giác chỉ chọn một góc ngoài).

Xem đáp án

Lời giải

Ta có: $∠ A_{1} + ∠ B_{1} + ∠ C_{1} + ∠ D_{1} = 360^{o}$ (tổng các góc của tứ giác)

+) Lại có: $∠ A_{1} + ∠ A_{2} = 180^{o}$ ( hai góc kề bù).

$∠ B_{1} + ∠ B_{2} = 180^{o}$ (hai góc kề bù)

$∠ C_{1} + ∠ C_{2} = 180^{o}$ (hai góc kề bù)

$∠ D_{1} + ∠ D_{2} = 180^{o}$ (hai góc kề bù)

Suy ra: $∠ A_{1} + ∠ A_{2}$ + $∠ B_{1} + ∠ B_{2}$ + $∠ C_{1} + ∠ C_{2}$ + $∠ D_{1} + ∠ D_{2}$ = $180^{0} . 4 = 720^{0}$

⇒ $∠ A_{2} + ∠ B_{2} + ∠ C_{2} + ∠ D_{2} = 720^{0} - (∠ A_{1} + ∠ B_{1} + ∠ C_{1} + ∠ D_{1})$

= $720^{0} - 360^{0} = 360^{0}$

Câu 3