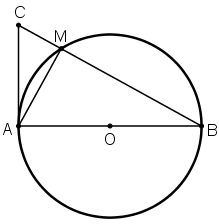
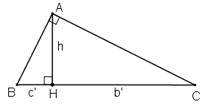
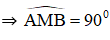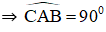Trên đường tròn (O) đường kính AB, lấy điểm M (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BM cắt tiếp tuyến đó tại C. Chứng minh rằng ta luôn có:
Quảng cáo
Trả lời:
Giải bởi Vietjack
là góc nội tiếp chắn nửa đường tròn
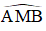
AC là tiếp tuyến của đường tròn tại A
⇒ AC ⊥ AO
⇒ ΔABC vuông tại A có đường cao AM
⇒ (Hệ thức về cạnh và đường cao trong tam giác vuông).
Kiến thức áp dụng
+ ΔABC vuông tại A có: h2 = b’.c’
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Tiếp tuyến của đường tròn (O) tại A là đường thẳng qua A và vuông góc với bán kính OA.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Hai cung bị chắn giữa hai dây song song thì bằng nhau.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
là góc nội tiếp chắn nửa đường tròn ⇒ 
⇒ AN ⊥ NB
là góc nội tiếp chắn nửa đường tròn ⇒ 
⇒ AM ⊥ MB
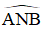
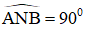
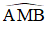
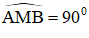
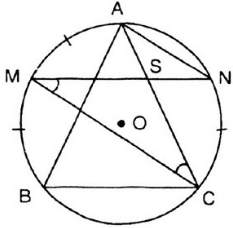
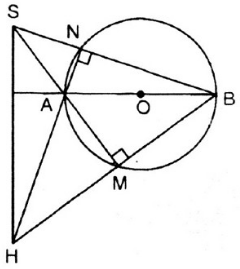
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
Kiến thức áp dụng
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Trong một tam giác, ba đường cao đồng quy tại trực tâm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập