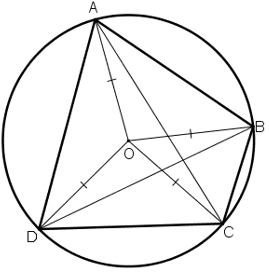
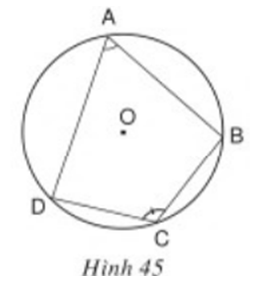
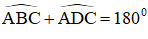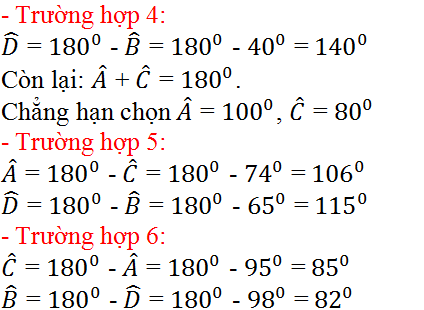Tứ giác ABCD có góc ABC + góc ADC = 180o. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm.
Quảng cáo
Trả lời:
Tứ giác ABCD có
⇒ ABCD là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
⇒ OA = OB = OC = OD = R
Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.
Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD
Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.
⇒ O thuộc đường trung trực của AC, BD, AB .
Vậy các đường trung trực của AC, BD, AB cùng đi qua O.
Kiến thức áp dụng
+ Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 180º thì tứ giác đó nội tiếp một đường tròn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
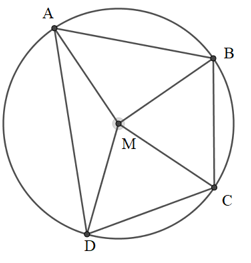
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
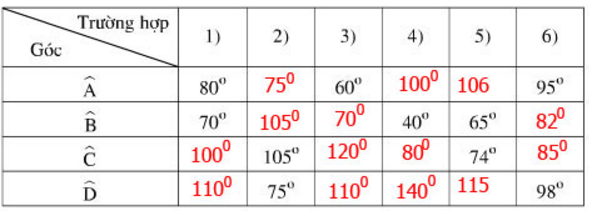
Tứ giác nội tiếp có tổng hai góc đối bằng nên:
- Điền vào ô trống:
- Cách tính:
Kiến thức áp dụng
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180º.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.