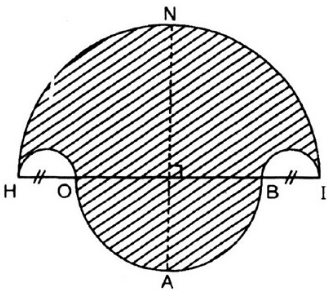
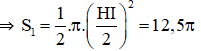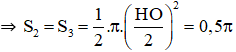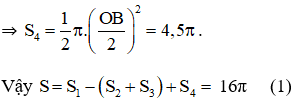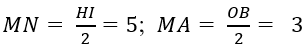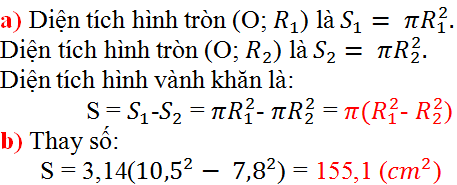a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.
b) Tính diện tích hình HOABINH (miền gạch sọc).
c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .
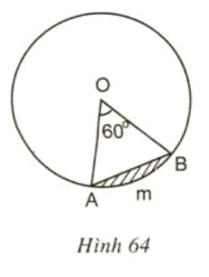
Hình 62
Quảng cáo
Trả lời:
a) Cách vẽ
- Vẽ nửa đường tròn đường kính HI = 10cm, tâm M.
- Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.
- Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).
- Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.
b)
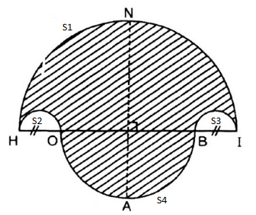
Diện tích miền gạch sọc bằng:
với:
+ là nửa đường tròn đường kính HI
+ là nửa đường tròn đường kính HO và BI.
+ Ta tính OB:
Ta có: HO+ OB + BI = HI
⇔ 2+ OB + 2= 10 nên OB = 6
+ S4 là nửa đường tròn đường kính OB
c)Ta có:
Do đó, NA = MN+ MA= 8
Diện tích hình tròn đường kính NA bằng :
so sánh (1) và (2) ta thấy hình tròn đường kính NA có cùng diện tích với hình HOABINH.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Kiến thức áp dụng
Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
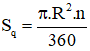
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.