Câu hỏi:
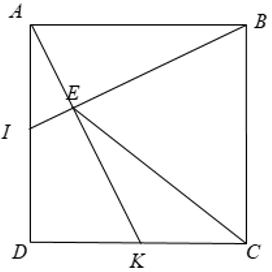
09/05/2025 5,629Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC. Chứng minh rằng BI ⊥ AK.
Câu hỏi trong đề: Tổng hợp lí thuyết và bài tập Toán 8 Chương 1: Tứ giác !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét △ BAI và △ ADK có
\(\left\{ \begin{array}{l}AB = AD\\AI = DK = \frac{1}{2}AB = \frac{1}{2}AD\\\widehat A = \widehat D = {90^ \circ }\end{array} \right.\)
△ BAI = △ ADK (c-g-c)
\(\widehat {ABI} = \widehat {DAK}\)(2 góc tương ứng)
Mà \(\widehat {IAE} + \widehat {EAB} = {90^ \circ }\) ⇒ \(\widehat {ABI} + \widehat {EAB} = {90^ \circ }\)
Xét ∆ ABE có
\(\widehat {ABE} + \widehat {EAB} + \widehat {AEB} = {180^ \circ }\)
\(\widehat {AEB} = {180^ \circ } - \widehat {ABE} + \widehat {EAB}\)
\(\widehat {AEB} = {180^ \circ } - {90^ \circ }\)= 90° hay BI ⊥ AK.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo