Câu hỏi trong đề: Bài tập ôn tập chương 3 đại số 9 có đáp án !!
Quảng cáo
Trả lời:
a) Giải hệ thứ nhất, ta được nghiệm duy nhất x = 2 và y = 1
Hai hệ tương đương khi (2;1) cũng là nghiệm của hệ còn lại, nghĩa là:
Thử lại với m = 3, hệ có dạng . Giải hệ này, ta có nghiệm duy nhất (2;1)
Vậy m = 3 thỏa yêu cầu.
b) Giải hệ thứ nhất, ta được nghiệm duy nhất x = -1 và y = 1.
Hai hệ tương đương khi (-1;1) là nghiệm của hệ còn lại, nghĩa là
Thử lại:
- Với m = 1 hệ có dạng . Hệ có vô số nghiệm nên m = 1 không thỏa mãn
- Với m = 6 hệ có dạng . Hệ có nghiệm duy nhất (-1;1)
Vậy m = 6 thỏa mãn yêu cầu.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
- Giải hệ thứ nhất, ta thấy hệ có vô số nghiệm thỏa mãn
- Giải hệ thứ hai, ta thấy hệ có vô số nghiệm thỏa mãn
Vậy hai hệ phương trình là tương đương.
Lời giải
a) Vì x + 2y = 9 là đường xiên, x = n là đường thẳng song song với Oy nên đồ thị của x + 2y = 9 luôn cắt đồ thị của x = n tại một điểm duy nhất
Vậy hệ luôn có nghiệm duy nhất x = n và

b) Vì 3x – 2y = 8 là đường xiên, y = m là đường thẳng song song với Ox nên đồ thị của 3x – 2y = 8 luôn cắt đồ thị của y = m tại một điểm duy nhất.
Vậy hệ luôn có nghiệm duy nhất y = m và
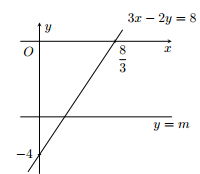
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.