Trong không gian tọa độ $Oxyz$, cho điểm $M(1;2;-3)$. Hình chiếu của M tương ứng lên $Ox,Oy,Oz,\left(Oyz\right),\left(Ozx\right),\left(Oxy\right)$là $A,B,C,D,E,F$. Gọi P và Q tương ứng là giao điểm của đường thẳng OM với các mặt phẳng $\left(ABC\right)$ và $\left(DEF\right)$. Độ dài PQ bằng:

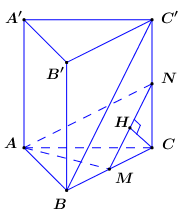
Gọi N là trung điểm của CC’ $\Rightarrow MN$ là đường trung bình của tam giác BCC’.

\[ \Rightarrow MN//BC' \Rightarrow BC'//\left( {AMN} \right) \supset AM\].

Khi đó ta có $d(AM;B{C}^{\text{'}})=d(B{C}^{\text{'}};\left(AMN\right))=d(B;\left(AMN\right))$.

Ta có: $BC\cap \left(AMN\right)=M\Rightarrow \frac{d(B;\left(AMN\right))}{d(C;\left(AMN\right))}=\frac{BM}{CM}=1$$\Rightarrow d(B;\left(AMN\right))=d(C;\left(AMN\right))$.

Trong (BCC’B’) kẻ $CH\perp MN(H\in MN)$ ta có:

$\{\begin{array}{l}AM\perp CM\\ AM\perp CN\end{array}\Rightarrow AM\perp \left(BC{C}^{\text{'}}{B}^{\text{'}}\right)\Rightarrow AM\perp CH$

$\{\begin{array}{l}CH\perp AM\\ CH\perp MN\end{array}\Rightarrow CH\perp \left(AMN\right)\Rightarrow d(C;\left(AMN\right))=CH$

$\Rightarrow d(AM;B{C}^{\text{'}})=CH$.

Áp dụng hệ thức lượng trong tam giác vuông CMN có: $CH=\frac{CM.CN}{\sqrt{C{M}^2+C{N}^2}}=\frac{\frac{a}{2}.\frac{a}{2}}{\sqrt{\frac{a^2}{4}+\frac{a^2}{4}}}=\frac{a\sqrt{2}}{4}$.

Vậy $d(AM;B{C}^{\text{'}})=\frac{a\sqrt{2}}{4}$.

Đáp án D.

Ta có:

$a+\frac{b+{\log }_{2}5}{c+{\log }_{2}3}={\log }_{6}45\iff a+\frac{b+{\log }_{2}5}{c+{\log }_{2}3}=\frac{{\log }_{2}45}{{\log }_{2}6}$

$\iff a+\frac{b+{\log }_{2}5}{c+{\log }_{2}3}=\frac{{\log }_2\left(3^2.5\right)}{{\log }_2\left(2.3\right)}\iff a+\frac{b+{\log }_{2}5}{c+{\log }_{2}3}=\frac{2{\log }_{2}3+{\log }_{2}5}{1+{\log }_{2}3}$

$\iff a+\frac{b+{\log }_{2}5}{c+{\log }_{2}3}=\frac{2+2{\log }_{2}3-2+{\log }_{2}5}{1+{\log }_{2}3}\iff a+\frac{b+{\log }_{2}5}{c+{\log }_{2}3}=2+\frac{-2+{\log }_{2}5}{1+{\log }_{2}3}$

Đồng nhất hệ số ta có $a=\mathrm{2,}b=-\mathrm{2,}c=1.$

Vậy  $a+b+c=2+(-2)+1=1.$

Đáp án A.