Câu hỏi:
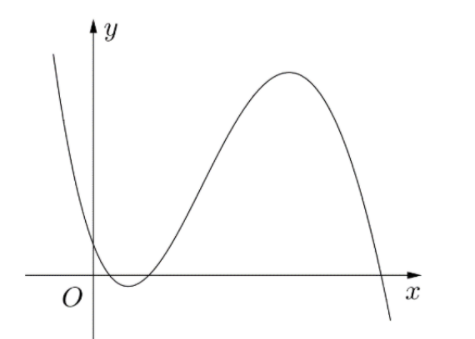
27/04/2022 2,385Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\left( {a \ne 0} \right)\) có đồ thị của đạo hàm \(f'\left( x \right)\) như hình vẽ. Biết rằng \(e >n.\)
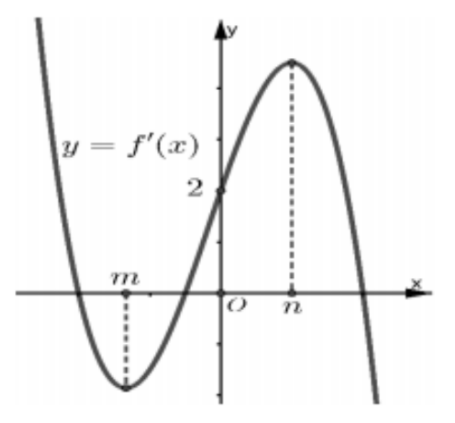
Số điểm cực trị của hàm số \(y = f'\left( {f\left( x \right) - 2x} \right)\) là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có:
Xét phương trình \(\left( 1 \right) \Leftrightarrow f'\left( x \right) = 2.\)
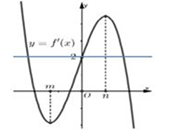
Từ đồ thị ta có phương trình \(\left( 1 \right)\) có 3 nghiệm phân biệt \({x_1},0,{x_2}\left( {{x_1} < m < 0 < n < {x_2}} \right).\)
Xét phương trình \(\left( 2 \right).\)
Trước hết ta có: \(f'\left( x \right) = 4a{x^3} + 3b{x^2} + 2cx + d.\)
\(f'\left( 0 \right) = 2 \Leftrightarrow d = 2.\)
Suy ra: \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + 2x + e.\)
\( \Leftrightarrow \left[ \begin{array}{l}a{x^4} + b{x^3} + c{x^2} = m - e{\rm{ }}\left( {2a} \right)\\a{x^4} + b{x^3} + c{x^2} = n - e{\rm{ }}\left( {2b} \right)\end{array} \right..\)
Số nghiệm của hai phương trình \(\left( {2a} \right)\) và \(\left( {2b} \right)\) lần lượt bằng số giao điểm của hai đường thẳng \(y = m - e\) và \(y = n - e\) (trong đó \(m - e < n - e < 0)\) với đồ thị hàm số \(g\left( x \right) = a{x^4} + b{x^3} + c{x^2}.\)
\(g'\left( x \right) = 4a{x^3} + 3b{x^2} + 2cx.\)
\(g'\left( x \right) = 0 \Leftrightarrow 4a{x^3} + 3b{x^2} + 2cx = 0 \Leftrightarrow 4a{x^3} + 3b{x^3} + 2cx + 2 = 2\)
\( \Leftrightarrow f'\left( x \right) = 2 \Leftrightarrow \left[ \begin{array}{l}x = {x_1} < 0\\x = 0\\x = {x_2} >0\end{array} \right.\)</>
Từ đồ thị hàm số \(y = f'\left( x \right)\) suy ra:
+) \(\mathop {\lim }\limits_{x \to - \infty } f'\left( x \right) = + \infty \) nên \(a < 0\) nên \(\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = - \infty ,\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = - \infty .\)
Bảng biến thiên của hàm số \(y = g\left( x \right):\)
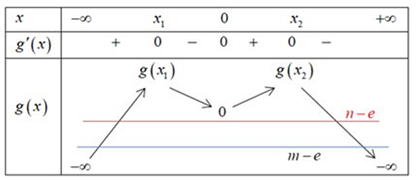
Từ bảng biến thiên suy ra hai phương trình \(\left( {2a} \right),\left( {2b} \right)\) mỗi phương trình có hai nghiệm phân biệt
(hai phương trình không có nghiệm trùng nhau) và khác \({x_1},0,{x_2}.\)
Suy ra phương trình có 7 nghiệm đơn phân biệt. Vậy hàm số \(y = f'\left[ {f\left( x \right) - 2x} \right]\) có 7 điểm cực trị.
Đáp án A
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Từ đồ thị ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0.\)
Gọi \({x_1}\) và \({x_2}\) lần lượt là hai điểm cực trị của hàm số đã cho \(\left( {{x_1} < {x_2}} \right).\)
Từ đồ thị ta thấy: \({x_1} + {x_2} >0 \Rightarrow ab < 0 \Rightarrow b >0.\)</>
Và: \({x_1}.{x_2} >0 \Rightarrow ac >0 \Rightarrow c >0.\)
Đồ thị hàm số giao với trục tung tại điểm có tung độ \(y \Rightarrow d >0.\)
Vậy trong các số \(a,b,c,d\) có hai số dương.
Đáp án D
Lời giải
Tập xác định \(D = \mathbb{R}\)
\(y' = 3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5\)
Hàm số đồng biến trong khoảng \(\left( {2; + \infty } \right)\) khi \(y' \ge 0,\forall x \in \left( {2; + \infty } \right).\)
\( \Leftrightarrow 3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5 \ge 0\forall x \in \left( {2; + \infty } \right).\)
\(3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5 \ge 0 \Leftrightarrow m \le \frac{{3{x^2} - 6x + 5}}{{12\left( {x - 1} \right)}},\forall x \in \left( {2; + \infty } \right)\)
Xét hàm số \(g\left( x \right) = \frac{{3{x^2} - 6x + 5}}{{12\left( {x - 1} \right)}},\forall x \in \left( {2; + \infty } \right).\)
\(g'\left( x \right) = \frac{{3{x^2} - 6x + 1}}{{12{{\left( {x - 1} \right)}^2}}} >0,\forall x \in \left( {2; + \infty } \right) \Rightarrow \) Hàm số \(g\left( x \right)\) đồng biến trong khoảng \(\left( {2; + \infty } \right).\)
Do đó: \(m \le g\left( x \right),\forall x \in \left( {2; + \infty } \right) \Rightarrow m \le g\left( 2 \right) \Leftrightarrow m \le \frac{5}{{12}}.\)
Vì \(0 < m \le \frac{5}{{12}}.\) Do đó không có giá trị nguyên dương nào của \(m\) thỏa mãn bài toán.
Đáp án C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận