Câu hỏi:
06/05/2022 534Một đề thi trắc nghiệm gồm 50 câu, mỗi câu có 4 phương án trả lời trong đó chỉ có 1 phương án đúng, mỗi câu trả lời đúng được 0,2 điểm. Một thí sinh làm bài bằng cách chọn ngẫu nhiên 1 trong 4 phương án ở mỗi câu. Tính xác suất để thí sinh đó được 6 điểm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp ánC.
Mỗi câu trả lời đúng được 0,2 điểm do vậy thí sinh được 6 điểm thì phải làm đúng số câu là \(\frac{6}{{0,2}} = 30\) câu
Mỗi câu có 4 phương án trả lời trong đó chỉ có 1 phương án đúng vì vậy xác suất trả lời đúng một câu là \(\frac{1}{4} = 0,25\) và xác suất trả lời sai một câu là \(\frac{3}{4} = 0,75\)
Số cách chọn 30 câu trả lời đúng trong 50 câu là \(C_{50}^{30}\)
Vậy xác suất để thí sinh đó được 6 điểm là \({0,25^{30}}{.0,75^{20}}.C_{50}^{30}.\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A.
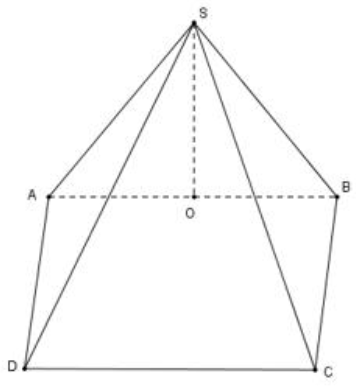
Vẽ đường cao
\(SO\) của tam giác đều \(SAB.\)
Ta có \(\left( {SAB} \right) \bot \left( {ABCD} \right) \Rightarrow SO \bot \left( {ABCD} \right).\)
Do đó \(SO\) là đường cao của hình nón \(S.ABCD\) và \(SO = \frac{{6a\sqrt 3 }}{2} = 3a\sqrt 3 .\)
Thể tích của khối chóp \(S.ABCD:V = \frac{1}{3}{S_{ABCD}}.SO = \frac{1}{3}.{\left( {6a} \right)^2}.3a\sqrt 3 = 36\sqrt 3 {a^3}.\)
Lời giải
Đáp án A.
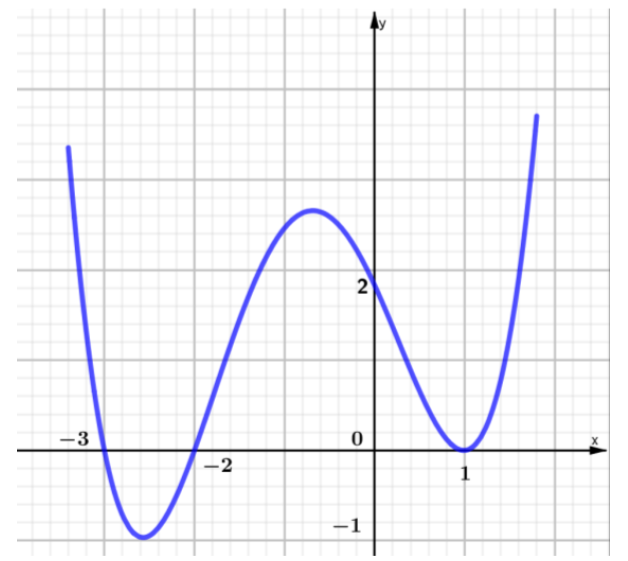
Phương trình hoành độ giao điểm của \(y = {x^3} - 2{x^2} + 3x - 2\) với trục hoành là
\({x^3} - 2{x^2} + 3x - 2 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - x + 2} \right) = 0 \Leftrightarrow x = 1\) (do \({x^2} - x + 2 >0,\forall x \in \mathbb{R}).\)
Vậy số giao điểm cần tìm là 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận