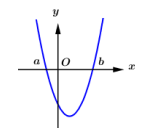
Cho tứ diện ABCD có cạnh AB, AC và AD đôi một vuông góc với nhau; AB = 6, AC = 7, AD = 4. Gọi M, N, P tương ứng là trung điểm các cạnh . Tính thể tích V của khối tứ diện ABCD.
Cho tứ diện ABCD có cạnh AB, AC và AD đôi một vuông góc với nhau; AB = 6, AC = 7, AD = 4. Gọi M, N, P tương ứng là trung điểm các cạnh . Tính thể tích V của khối tứ diện ABCD.
A.
B. V = 7
C.
D. V = 14
Quảng cáo
Trả lời:
Phương pháp:
- Hai khối chóp có cùng chiều cao thì tỉ số thể tích bằng tỉ số diện tích đáy.
- Sử dụng tam giác đồng dạng để suy ra tỉ số diện tích đáy.
Cách giải:
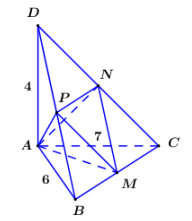
Hai khối chóp A.BCD và A.MNP có cùng chiều cao là khoảng cách từ A đến (BCD) nên
Dễ thấy tam giác MNP đồng dạng tam giác DBC theo tỉ số nên
Mà
Vậy
Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
Lập bảng biến thiên của hàm số y = f(x) và y = g(x).
Cách giải:
Dựa vào đồ thị hàm số ta có bảng biến thiên của y = f(x) như sau:
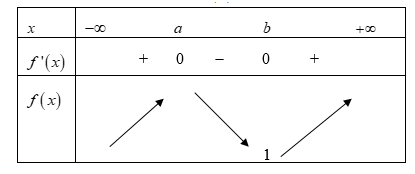
Đặt ta có:
Hàm số y = h(x) có 3 điểm cực trị Hàm số y = h(x) + m cũng có 3 điểm cực trị.
Vì số điểm cực trị của hàm số bằng tổng số điểm cực trị của hàm số y = h(x) + m và số giao điểm của đồ thị hàm số y = h(x) + m với trục hoành (không tính tiếp xúc).
Nên để hàm số có 5 điểm cực trị thì phương trình h(x) = 0 có 2 nghiệm phân biệt (không tính nghiệm kép).
Bảng biến thiên hàm số h(x) như sau:
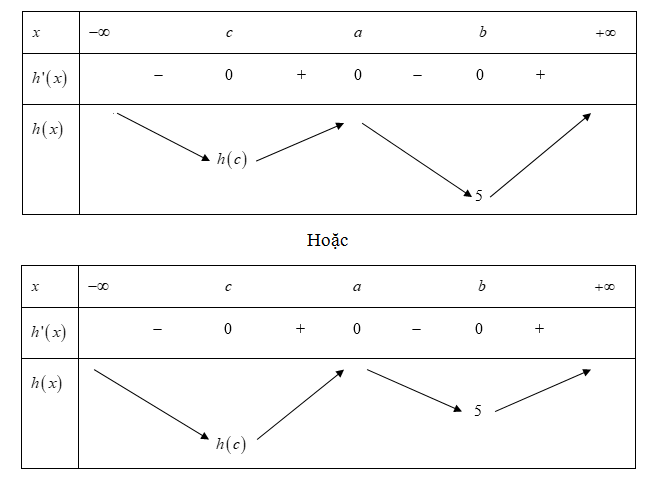
với
Nếu h(c) > 5 thì phương trình h(x) = -m có 2 nghiệm phân biệt (không tính nghiệm kép)
(không thỏa mãn ).
Nếu thì phương trình h(x) = -m có 2 nghiệm phân biệt (không tính nghiệm kép)
(thỏa mãn ).
Mà
Vậy có 10 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn A.
Lời giải
Phương pháp:
Áp dụng công thức tính tổ hợp.
Cách giải:
Số tập con có 3 phần tử của tập hợp 7 phần tử là
Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.