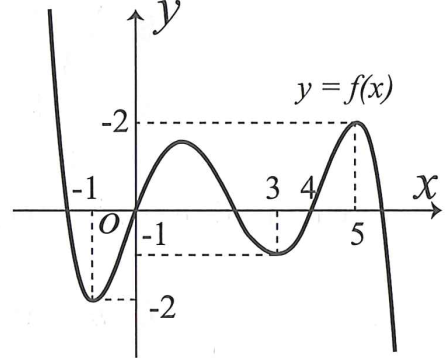
Cho hàm số f(x) có đạo hàm trên R thỏa mãn . Đặt , m là tham số nguyên và m<27. Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số g(x) đạt cực tiểu tại x=0. Tính tổng bình phương các phần tử của S.
Cho hàm số f(x) có đạo hàm trên R thỏa mãn . Đặt , m là tham số nguyên và m<27. Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số g(x) đạt cực tiểu tại x=0. Tính tổng bình phương các phần tử của S.
Quảng cáo
Trả lời:
Đáp án A
Từ giả thiết ta có: .
(C là hằng số).
Ta có:
.
Khi đó:
TH1: m=2, ta có: .
Vì x=0 là nghiệm bội chẵn của phương trình g'(x)=0 nên trường hợp này loại.
TH2: m=5 ta có: .
TH3: m=-2, ta có: .
Vì x=0 là nghiệm bội chẵn của phương trình g'(x) nên m=-2 không thỏa mãn.
TH4:m=5 ta có: .
Do đổi dấu từ âm sang dương khi qua nên hàm số đạt cực tiểu tại .
TH5: ta có: .
Do g'(x) đổi dấu từ âm sang dương khi qua x=0 nên hàm số đạt cực tiểu tại x=0.
Vậy nên tổng các bình phương của các phần tử của S là 100.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án B
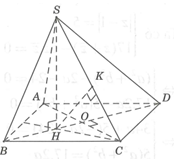
Xác định và .
Ta có .
Ta có: .
Kẻ . Khi đó .
Tam giác vuông SHC, có .
Vậy .
Lời giải
Đáp án A
Ta có:
Để hàm số nghịch biến trên đoạn có độ dài bằng 2 thì có hai nghiệm phân biệt thỏa mãn: .
Ta có: .
Để có hai nghiệm phân biệt thì .
Theo định lý Vi-ét, ta có:
Theo bài ra ta có:Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
D. 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.