Câu hỏi:

19/05/2022 309

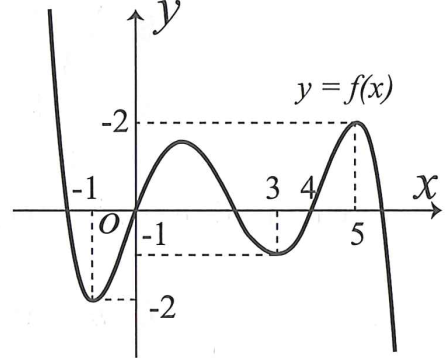
Cho cấp số cộng $(a_{n})$ , cấp số nhân $(b_{n})$ thỏa mãn $a_{2} > a_{1} \geq 0, b_{2} > b_{1} \geq 1$ và hàm số $f (x) = x^{3} - 3 x$ sao cho $f (a_{2}) + 2 = f (a_{1})$ và $f (\log_{2} b_{2}) + 2 = f (\log_{2} b_{1})$ . Tìm số nguyên dương n nhỏ nhất sao cho $b_{n} > 2019 a_{n}$ .

A. 17.

B. 14.

C. 15.

D. 16.

Xem lời giải

Câu hỏi trong đề: Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án D

Xét hàm số $f (x) = x^{3} - 3 x$ trên $[0; + \infty)$ .

Ta có $f' (x) = 3 x^{2} - 3 = 0 \Leftrightarrow [\begin{array}{l} x = 1 \in [0; + \infty) \\ x = - 1 \notin [0; + \infty) \end{array} .$

Bảng biến thiên hàm số f(x) trên $[0; + \infty)$ như sau:

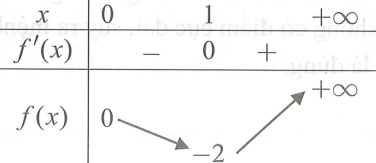
Cho cấp số cộng (an) , cấp số nhân (bn) thỏa mãn a2>a1>=0, b2>b1>=1 và hàm số f(x)=x^2-3x sao cho f(a1)+2=f(a1) và f(log2b1)+2=f(log2b1). Tìm số nguyên dương n nhỏ nhất sao cho bn>2019an . (ảnh 1)

Vì $a_{2} > 0$ nên $f (a_{2}) \geq - 2 \Rightarrow f (a_{1}) = f (a_{2}) + 2 \geq 0 (1) .$

Giả sử $a_{1} \geq 1$ , vì $f (x)$ đồng biến trên $[1; + \infty)$ nên $f (a_{2}) > f (a_{1})$ suy ra $f (a_{2}) + 2 > f (a_{1})$ vô lý.

Vậy $a_{1} \in [0; 1)$ do đó $- 2 \leq f (a_{1}) \leq 0 (2) .$

Từ (1), (2) ta có: $\{\begin{cases} f (a_{1}) = 0 \\ f (a_{2}) = - 2 \end{cases} \Leftrightarrow \{\begin{cases} a_{1} = 0 \\ a_{2} = 1 \end{cases} .$

Vậy số hạng tổng quát của dãy cấp số cộng $(a_{n})$ là: $a_{n} = n - 1.$

Đặt $\{\begin{cases} t_{1} = \log_{2} b_{1} \\ t_{2} = \log_{2} b_{2} \end{cases}$ , suy ra: $f (t_{1}) = f (t_{2}) + 2$ , vì $1 \leq b_{1} < b_{2}$ nên $0 \leq t_{1} < t_{2}$ , theo lập luận trên ta có: $\{\begin{cases} t_{1} = 0 \\ t_{2} = 1 \end{cases} \Leftrightarrow \{\begin{cases} \log_{2} b_{1} = 0 \\ \log_{2} b_{2} = 1 \end{cases} \Leftrightarrow \{\begin{cases} b_{1} = 1 \\ b_{2} = 2 \end{cases} .$

Vậy số hạng tổng quát của dãy cấp số nhân $(b_{n})$ là $b_{n} = 2^{n - 1}$ .

Do đó $b_{n} > 2019 a_{n} \Leftrightarrow 2^{n - 1} > 2019 (n - 1) (*)$ .

Trong 4 đáp án n=16 là số nguyên dương nhỏ nhất thỏa mãn (*).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng (ABCD) góc $30 °$ . Tính khoảng cách d từ B đến mặt phẳng (SDC) theo a.

d = \frac{2 a \sqrt{21}}{21} .

d = \frac{a \sqrt{21}}{7} .

d = a .

d = a \sqrt{3} .

Lời giải

Đáp án B

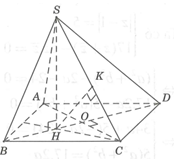
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng (ABCD) góc 30 độ . Tính khoảng cách d từ B đến mặt phẳng (SCD) theo a. (ảnh 1)

Xác định $30 ° = \hat{S D, (A B C D)} = \hat{S D, H D} = \hat{S D H}$ và $S H = H D . \tan \hat{S D H} = \frac{2 a}{3}$ .

Ta có $d (B, (S C D)) = \frac{B D}{H D} . d (H, (S C D)) = \frac{3}{2} . d (H, (S C D))$ .

Ta có: $H C ⊥ A B \Rightarrow H C ⊥ C D$ .

Kẻ $H K ⊥ S C$ . Khi đó $d (H, (S C D)) = H K$ .

Tam giác vuông SHC, có $H K = \frac{S H . H C}{\sqrt{S H^{2} + H C^{2}}} = \frac{2 a \sqrt{21}}{21}$ .

Vậy $d (B, (S C D)) = \frac{3}{2} H K = \frac{a \sqrt{21}}{7}$ .

Câu 2

Tìm tất cả các giá trị của m để hàm số $y = x^{3} - 3 m x^{2} + 3 (2 m - 1) x + 1$ nghịch biến trên đoạn có độ dài bằng 2?

m = 0, m = 2.

m = 1.

m = 0.

m = 2.

Lời giải

Đáp án A

Ta có: $y' = 3 x^{2} - 6 m x + 3 (2 m - 1)$

Để hàm số nghịch biến trên đoạn có độ dài bằng 2 thì $y' = 0$ có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn: $|x_{1} - x_{2}| = 2$ .

Ta có: $Δ' = 9 m^{2} - 9 (2 m - 1) = 9 {(m - 1)}^{2}$ .

Để $y' = 0$ có hai nghiệm phân biệt $x_{1}, x_{2}$ thì $Δ' > 0 \Leftrightarrow 9 {(m - 1)}^{2} > 0 \Leftrightarrow m \neq 1$ .

Theo định lý Vi-ét, ta có: $\{\begin{cases} x_{1} + x_{2} = 2 m \\ x_{1} x_{2} = 2 m - 1 \end{cases} .$

Theo bài ra ta có:

|x_{1} - x_{2}| = 2 \Leftrightarrow {(x_{1} - x_{2})}^{2} = 4 \Leftrightarrow {(x_{1} + x_{2})}^{2} - 4 x_{1} x_{2} = 4 \Leftrightarrow 4 m^{2} - 8 m = 0 \Leftrightarrow [\begin{array}{l} m = 0 \\ m = 2 \end{array} .

Câu 3

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB=a, BC=2a . Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD), cạnh $S A = a \sqrt{15}$ . Tính góc tạo bởi đường thẳng SC và mặt phẳng (ABD).

30 ° .

45 ° .

60 ° .

90 ° .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Có bao nhiêu giá trị m để đồ thị hàm số $y = \frac{m x^{2} - 1}{x^{2} - 3 x + 2}$ có đúng hai đường tiệm cận?

A. 1

B. 2

C. 3

D. 4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số f(x) có đồ thị như hình vẽ:

Có bao nhiêu giá trị nguyên của $m \in (- 10; 10)$ để $f (\sqrt{x^{2} + 2 x + 10}) - 3 = m$ có nghiệm?

A. 8.

B. 6.

C. 9.

D. 7.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số $y = |\frac{1}{4} x^{4} - \frac{19}{2} x^{2} + 30 x + m|$ trên đoạn $[0; 2]$ đạt giá trị nhỏ nhất?

A. 2.

B. 3.

C. 0.

D. 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian với hệ tọa độ Oxyz, lập phương trình của các mặt phẳng song song với mặt phẳng $(β) : x + y - z + 3 = 0$ và cách $(β)$ một khoảng bằng $\sqrt{3}$ .

x + y - z + 6 = 0

và

x + y - z = 0

x + y - z + 6 = 0

x - y - z + 6 = 0

và

x - y - z = 0

x + y + z + 6 = 0

và

x + y + z = 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Cho cấp số cộng an , cấp số nhân bn thỏa mãn a2>a1≥0, b2>b1≥1 và hàm số fx=x3−3x sao cho fa2+2=fa1 và flog2b2+2=flog2b1 . Tìm số nguyên dương n nhỏ nhất sao cho bn>2019an .

Tìm tất cả các giá trị của m để hàm số y=x3−3mx2+32m−1x+1 nghịch biến trên đoạn có độ dài bằng 2?

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB=a, BC=2a . Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD), cạnh SA=a15 . Tính góc tạo bởi đường thẳng SC và mặt phẳng (ABD).

Có bao nhiêu giá trị m để đồ thị hàm số y=mx2−1x2−3x+2 có đúng hai đường tiệm cận?

Cho hàm số f(x) có đồ thị như hình vẽ: Có bao nhiêu giá trị nguyên của m∈−10;10 để fx2+2x+10−3=m có nghiệm?

Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y=14x4−192x2+30x+m trên đoạn 0;2 đạt giá trị nhỏ nhất?

Trong không gian với hệ tọa độ Oxyz, lập phương trình của các mặt phẳng song song với mặt phẳng β:x+y−z+3=0 và cách β một khoảng bằng 3 .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tìm tất cả các giá trị của m để hàm số $y = x^{3} - 3 m x^{2} + 3 (2 m - 1) x + 1$ nghịch biến trên đoạn có độ dài bằng 2?

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB=a, BC=2a . Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD), cạnh $S A = a \sqrt{15}$ . Tính góc tạo bởi đường thẳng SC và mặt phẳng (ABD).

Có bao nhiêu giá trị m để đồ thị hàm số $y = \frac{m x^{2} - 1}{x^{2} - 3 x + 2}$ có đúng hai đường tiệm cận?

Cho hàm số f(x) có đồ thị như hình vẽ:

Có bao nhiêu giá trị nguyên của $m \in (- 10; 10)$ để $f (\sqrt{x^{2} + 2 x + 10}) - 3 = m$ có nghiệm?

Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số $y = |\frac{1}{4} x^{4} - \frac{19}{2} x^{2} + 30 x + m|$ trên đoạn $[0; 2]$ đạt giá trị nhỏ nhất?

Trong không gian với hệ tọa độ Oxyz, lập phương trình của các mặt phẳng song song với mặt phẳng $(β) : x + y - z + 3 = 0$ và cách $(β)$ một khoảng bằng $\sqrt{3}$ .