Câu hỏi:
23/05/2022 267
Một thừa đất hình chữ nhật có chiều dài bằng 20 mét và chiều rộng bằng 10 mét, người ta giảm chiều dài \(x\) mét (với \(0\, < \,x\, < \,20\)) và tăng chiều rộng thêm 2x mét để được thửa đất mới. Tìm \(x\) để thửa đất mới có diện tích lớn nhất?
Một thừa đất hình chữ nhật có chiều dài bằng 20 mét và chiều rộng bằng 10 mét, người ta giảm chiều dài \(x\) mét (với \(0\, < \,x\, < \,20\)) và tăng chiều rộng thêm 2x mét để được thửa đất mới. Tìm \(x\) để thửa đất mới có diện tích lớn nhất?
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
Phương pháp giải: - Tính chiều dài, chiều rộng mới của thửa đất sau đó tính diện tích mới của thửa đất
- Sử dụng phương pháp hàm số tìm GTLN
Giải chi tiết:
Chiều dài mới của thửa đất là \(20 - x\)(mét)
Chiều rộng của thửa đất là \(10 + 2x\) (mét)
Khi đó diện tích mới của thửa đất là \(S = (20 - x)(10 + 2x)\)
Ta có:
\(S' = 0 \Leftrightarrow x = \frac{{15}}{2}\)
Ta có BBT như sau:
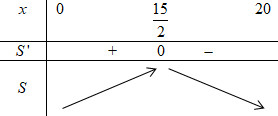
Vậy
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hai dao động điều hoà cùng phương, cùng tần số có biên độ và pha ban đầu lần lượt là A1, A2, φ1, φ2. Dao động tổng hợp của hai dao động trên có biên độ được tính theo công thức
Xem đáp án »
24/05/2022
10,930
Câu 2:
Theo số liệu từ Tổng cục thống kê, dân số Việt Nam năm 2015 là 91,7 triệu người. Giả sử tỉ lệ tăng dân số hàng năm của Việt Nam trong giai đoạn 2015 – 2050 ở mức không đổi là 1,1%. Hỏi đến năm nào dân số Việt Nam sẽ đạt mức 120,5 triệu người?
Xem đáp án »
23/05/2022
6,583
Câu 3:
Một chất điểm chuyển động theo quy luật \(S\,\left( t \right)\, = \,1\, + \,3{t^2}\, - \,{t^3}.\) Vận tốc của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu?
Xem đáp án »
25/05/2022
5,100
Câu 4:
Tác phẩm nào sau đây KHÔNG thuộc về khuynh hướng văn học hiện thực?
Xem đáp án »
23/05/2022
4,389
Câu 5:
Tập hợp các giá trị m để hàm số đồng biến trên \(\left( {6\,;\,7} \right)\) là
Xem đáp án »
25/05/2022
3,816
Câu 6:
Cho \(a\,,\,b\)là các số nguyên và . Tính \(P\, = \,{a^2}\, + \,{b^2}\, - \,a\, - \,b\).
Cho \(a\,,\,b\)là các số nguyên và . Tính \(P\, = \,{a^2}\, + \,{b^2}\, - \,a\, - \,b\).
Xem đáp án »
12/07/2024
3,791
Câu 7:
Một xe mô tô đang chạy với vận tốc \(20m/s\) thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh. Từ thời điểm đó, mô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right)\, = \,20\, - \,5t\), trong đó t là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh đến lúc mô tô dừng lại là
Xem đáp án »
23/05/2022
3,147
Bình luận
🔥 Đề thi HOT:
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Nghĩa của từ
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Câu hỏi điền từ
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
về câu hỏi!