Nêu định nghĩa tâm sai của elip có phương trình chính tắc là x2a2+y2b2=1 với a > b > 0.

Tâm sai e của elip có phương trình chính tắc là x2a2+y2b2=1 với a > b > 0 là tỉ số giữa tiêu cự và độ dài trục lớn của elip, tức là e=ca=a2−b2a.

Câu hỏi:

11/07/2024 567

Nêu định nghĩa tâm sai của elip có phương trình chính tắc là $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ với a > b > 0.

Xem lời giải

Câu hỏi trong đề: Bài tập Chuyên đề Hypebol có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

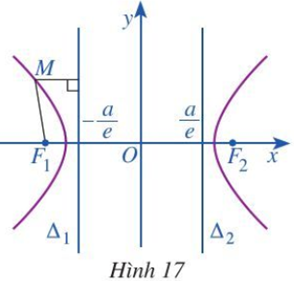
Tâm sai e của elip có phương trình chính tắc là $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ với a > b > 0 là tỉ số giữa tiêu cự và độ dài trục lớn của elip, tức là $e = \frac{c}{a} = \frac{\sqrt{a^{2} - b^{2}}}{a} .$

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong mặt phẳng tọa độ Oxy, cho hypebol $(H) : \frac{x^{2}}{64} - \frac{y^{2}}{36} = 1$ . Lập phương trình chính tắc của elip (E), biết rằng (E) có các tiêu điểm là các tiêu điểm của (H) và các đỉnh của hình chữ nhật cơ sở của (H) đều nằm trên (E).

Xem đáp án

Lời giải

Hypebol (H) có a = 8, b = 6 $\Rightarrow c = \sqrt{a^{2} + b^{2}} = 10$ và một đỉnh của hình chữ nhật cơ sở là M(8; 6).

Gọi phương trình chính tắc của elip cần tìm là $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ (a > b > 0).

Theo đề bài ta có:

+) (E) có các tiêu điểm là các tiêu điểm của (H) $\Rightarrow c = 10 \Rightarrow a^{2} - b^{2} = c^{2} = 100 (1) .$

+) Các đỉnh của hình chữ nhật cơ sở của (H) đều nằm trên (E) $\Rightarrow M (8; 6) \in (E)$

$\Rightarrow \frac{8^{2}}{a^{2}} + \frac{6^{2}}{b^{2}} = 1 \Rightarrow \frac{64}{a^{2}} + \frac{36}{b^{2}} = 1 (2) .$

Thế (1) vào (2) ta được:

$\frac{64}{b^{2} + 100} + \frac{36}{b^{2}} = 1 \Rightarrow \frac{64 b^{2} + 36 (b^{2} + 100)}{(b^{2} + 100) b^{2}} = 1$

$\Rightarrow 64 b^{2} + 36 (b^{2} + 100) = (b^{2} + 100) b^{2}$

$\Rightarrow 100 b^{2} + 3600 = b^{4} + 100 b^{2} \Rightarrow b^{4} = 3600 \Rightarrow b^{2} = 60 \Rightarrow a^{2} = 160.$

Vậy phương trình chính tắc của elip cần tìm là $\frac{x^{2}}{160} + \frac{y^{2}}{60} = 1.$

Câu 2

Dọc theo bờ biển, người ta thiết lập hệ thống định vị vô tuyến dẫn đường tầm xa để truyền tín hiệu cho máy bay hoặc tàu thuỷ hoạt động trên biển. Trong hệ thống đó có hai đài vô tuyến đặt lần lượt tại địa điểm A và địa điểm B, khoảng cách AB = 650 km (Hình 18). Giả sử có một con tàu chuyển động trên biển với quỹ đạo là hypebol nhận A và B là hai tiêu điểm.

Khi đang ở vị trí P, máy thu tín hiệu trên con tàu chuyển đổi chênh lệch thời gian nhận các tín hiệu từ A và B thành hiệu khoảng cách |PA – PB|. Giả sử thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A là 0,0012 s. Vận tốc di chuyển của tín hiệu là 3 . 10⁸ m/s.

a) Lập phương trình hypebol mô tả quỹ đạo chuyển động của con tàu.

b) Chứng tỏ rằng tại mọi thời điểm trên quỹ đạo chuyển động thì thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A luôn là 0,0012 s.

Xem đáp án

Lời giải

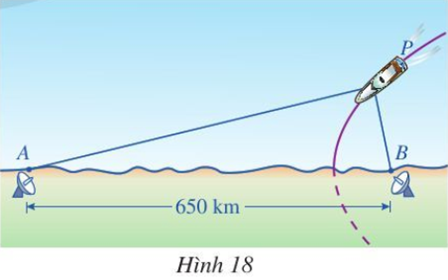
a) Vì thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A là 0,0012 s nên tại thời điểm đó PB – PA = (3 . 10⁸) . 0,0012 = 360000 (m) = 360 (km).

Vì con tàu chuyển động với quỹ đạo là hypebol nhận A và B là hai tiêu điểm nên |PA – PB| = 360 (km) với mọi vị trí của P.

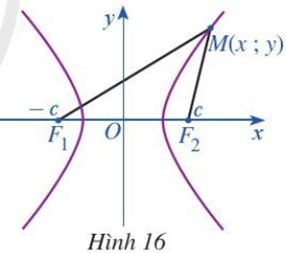
Chọn hệ trục toạ độ sao cho gốc toạ độ trùng với trung điểm của AB và trục Ox trùng với AB, đơn vị trên hai trục là km thì hypebol này có dạng $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ (a > 0, b > 0).

Vì |PA – PB| = 360 nên 2a = 360, suy ra a =180.

Theo đề bài, AB = 650, suy ra 2c = 650, suy ra c = 325.

b² = c² – a² = 325² – 180² = 73225.

Vậy phương trình hypebol mô tả quỹ đạo chuyển động của con tàu là $\frac{x^{2}}{32400} - \frac{y^{2}}{73225} = 1.$

b) Vì con tàu chỉ chuyển động ở nhánh bên phải trục Oy của hypebol nên ta PB < PA với mọi vị trí của P. Do đó tàu luôn nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A.

Gọi t₁ là thời gian để tàu nhận được tín hiệu từ A, t₂ là thời gian để tàu nhận được tín hiệu từ B thì $t_{1} = \frac{P A}{v}, t_{2} = \frac{P B}{v}$ với v là vận tốc di chuyển của tín hiệu.

Khi đó, ta có:

t₁ – t₂ = $\frac{P A - P B}{v} = \frac{360000}{3 . 8^{10}} = 0, 0012 (s) .$

Vậy thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A luôn là 0,0012 s.

Câu 3

Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc $\frac{x^{2}}{4} - \frac{y^{2}}{1} = 1$ .

a) Xác định toạ độ các đỉnh, tiêu điểm, tiêu cự, độ dài trục thực của hypebol.

b) Xác định phương trình các đường tiệm cận của hypebol và vẽ hypebol trên.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hypebol (H) có phương trình chính tắc $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ với a > 0, b > 0. Xét đường thẳng $Δ_{1} : x = - \frac{a}{e}$ .

Với mỗi điểm M (x₀; y₀) $\in$ (H) (Hình 17), tính:

a) Khoảng cách d (M, Δ₁) từ điểm M(x₀; y₀) đến đường thẳng Δ₁.

b) Tỉ số $\frac{M F_{1}}{d (M, Δ_{1})}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hypebol có phương trình chính tắc $\frac{x^{2}}{144} - \frac{y^{2}}{25} = 1.$ Giả sử M là điểm thuộc hypebol có hoành độ là 15. Tìm độ dài các bán kính qua tiêu của điểm M.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a, ở đó F₁F₂ = 2c với c > a > 0. Ta chọn hệ trục toạ độ Oxy có gốc là trung điểm của đoạn thẳng F₁F₂. Trục Oy là đường trung trực của F₁F₂ và F₂ nằm trên tia Ox (Hình 16). Khi đó F₁(c; 0), F₂(c; 0) là các tiêu điểm của (H).

Với mỗi điểm M(x; y) thuộc đường hypebol (H), chứng minh:

a) MF₁² = x² + 2cx + c² + y²;

b) MF₂² = x² – 2cx + c² + y²;

c) MF₁² – MF₂² = 4cx.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Vẽ hypebol $(H) : \frac{x^{2}}{9} - \frac{y^{2}}{16} = 1$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Nêu định nghĩa tâm sai của elip có phương trình chính tắc là x2a2+y2b2=1 với a > b > 0.

Bình luận

Trong mặt phẳng tọa độ Oxy, cho hypebol (H):x264−y236=1. Lập phương trình chính tắc của elip (E), biết rằng (E) có các tiêu điểm là các tiêu điểm của (H) và các đỉnh của hình chữ nhật cơ sở của (H) đều nằm trên (E).

Cho hypebol (H) có phương trình chính tắc x2a2−y2b2=1 với a > 0, b > 0. Xét đường thẳng Δ1:x=−ae. Với mỗi điểm M (x0; y0)∈(H) (Hình 17), tính: a) Khoảng cách d (M, Δ1) từ điểm M(x0; y0) đến đường thẳng Δ1. b) Tỉ số MF1dM,Δ1.

Cho hypebol có phương trình chính tắc x2144−y225=1. Giả sử M là điểm thuộc hypebol có hoành độ là 15. Tìm độ dài các bán kính qua tiêu của điểm M.

Vẽ hypebol (H):x29−y216=1.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Nêu định nghĩa tâm sai của elip có phương trình chính tắc là $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ với a > b > 0.

Cho hypebol có phương trình chính tắc $\frac{x^{2}}{144} - \frac{y^{2}}{25} = 1.$ Giả sử M là điểm thuộc hypebol có hoành độ là 15. Tìm độ dài các bán kính qua tiêu của điểm M.

Vẽ hypebol $(H) : \frac{x^{2}}{9} - \frac{y^{2}}{16} = 1$ .