Bài tập Elip có đáp án
48 người thi tuần này 4.6 1.3 K lượt thi 18 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
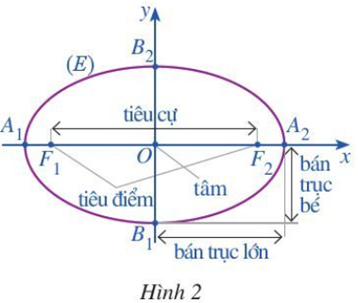
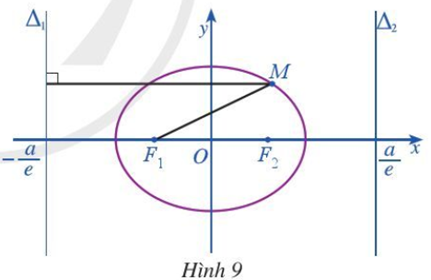
a) Toạ độ hai tiêu điểm F1, F2 của (E) là F1 F2
b)
+) Vì A2 thuộc trục Ox nên toạ độ của A2 có dạng
Mà A2 thuộc (E) nên
Ta thấy A2 nằm bên phải điểm O trên trục Ox nên A2(a; 0). Khi đó OA2 = (vì a > 0).
Vậy OA2 = a.
+) Vì B2 thuộc trục Oy nên toạ độ của B2 có dạng
Mà B2 thuộc (E) nên
Ta thấy B2 nằm bên trên điểm O trên trục Oy nên B2(0; b). Khi đó OB2 = (vì b > 0).
Vậy OB2 = b.
Lời giải
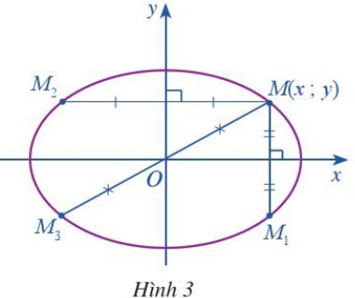
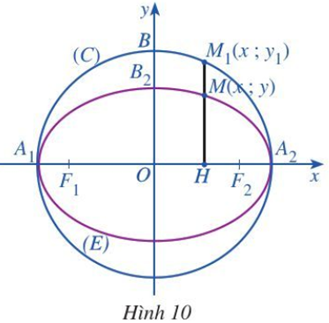
Theo đề bài, M(x; y) nằm trên (E) nên ta có:
a) M1 là điểm đối xứng của M qua trục Ox, suy ra M1 có toạ độ là (x; –y).
Ta có Do đó M1 cũng thuộc (E).
b) M2 là điểm đối xứng của M qua trục Oy, suy ra M2 có toạ độ là (–x; y).
Ta có Do đó M2 cũng thuộc (E).
c) M3 là điểm đối xứng của M qua gốc O, suy ra M3 có toạ độ là (–x; –y).
Ta có Do đó M3 cũng thuộc (E).
Lời giải
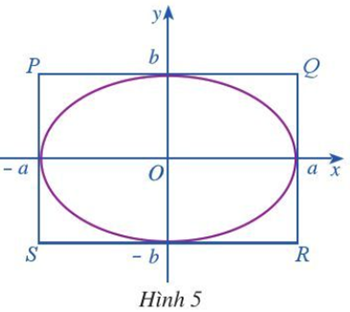
a) Bốn đỉnh của elip là trung điểm các cạnh của hình chữ nhật cơ sở.
b) Nếu điểm M(x; y) thuộc (E) thì
+) Vì nên –a ≤ x ≤ a.
Do đó:
Giá trị nhỏ nhất của x là –a khi x = –a, y = 0.
Giá trị lớn nhất của x là a khi x = a, y = 0.
+) Vì nên – b ≤ y ≤ b.
Do đó:
Giá trị nhỏ nhất của y là –b khi x = 0, y = –b.
Giá trị lớn nhất của y là b khi x = 0, y = b.
Lời giải
Gọi phương trình chính tắc của elip đã cho là (a > b > 0).
Elip đã cho có hai đỉnh là A1(– 4; 0) và B2(0; 2) nên a = 4, b = 2 hoặc a = 2, b = 4.
Mà a > b nên a = 4, b = 2.
Vậy phương trình chính tắc của elip đã cho là hay
Lời giải
a) Ta thấy Q(a; b), R(a; –b) nên QR =
Ta thấy P(–a; b), Q(a; b) nên PQ =
Vậy
b) Tỉ số phản ánh cụ thể hình dạng của (E) như sau:
– Nếu tỉ số càng bé thì hình chữ nhật cơ sở càng "dẹt", do đó (E) càng "gầy".
– Nếu tỉ số càng lớn thì b càng gần a và hình chữ nhật cơ sở càng gần với hình vuông, do đó (E) càng "béo".
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.