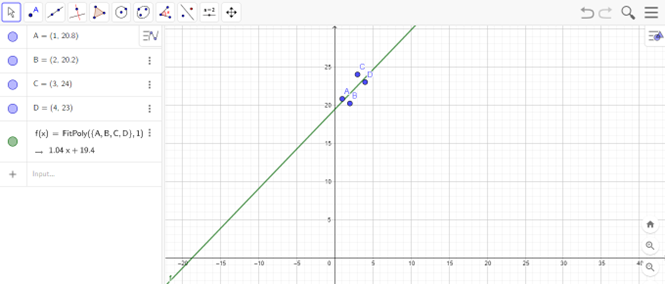
Bài tập Chủ đề 2. Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng có đáp án
32 người thi tuần này
4.6
817 lượt thi
2 câu hỏi
🔥 Đề thi HOT:
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
7.3 K lượt thi
13 câu hỏi
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
6.4 K lượt thi
16 câu hỏi
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
1.3 K lượt thi
12 câu hỏi
75 câu trắc nghiệm Vectơ nâng cao (P1)
41.1 K lượt thi
25 câu hỏi
15 câu Trắc nghiệm Toán 10 Kết nối tri thức Số gần đúng và sai số có đáp án
1.6 K lượt thi
15 câu hỏi
Bài tập Xác định tính hợp lí của dữ liệu trong bảng thống kê (có lời giải)
1.3 K lượt thi
5 câu hỏi
Đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 1
3.2 K lượt thi
37 câu hỏi
15 câu Trắc nghiệm Toán 10 Kết nối tri thức Hàm số có đáp án
2.6 K lượt thi
15 câu hỏi
Đề thi liên quan:
Danh sách câu hỏi:
4.6
163 Đánh giá
50%
40%
0%
0%
0%