Giải SBT Toán 10 CD Bài 1. Định lí côsin và định lí sin trong tam giác. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án
32 người thi tuần này 4.6 1.2 K lượt thi 11 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Lời giải
Đáp án đúng là B
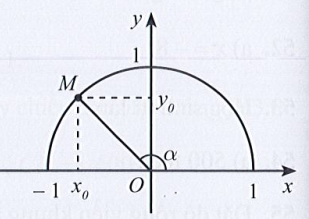
Với 0° < α < 180°, ta có:
– 1 < cosα < 1. Suy ra A sai.
0 < sinα < 1. Suy ra B đúng.
Do đó C và D sai.
Lời giải
Lời giải
Đáp án đúng là A
Ta có α + β = 180° nên ta có:
sinα = sinβ ⇒ sinα + sinβ = sinα + sinα = 2sinα
Vì 0° < α, β < 180° nên sinα ≠ 0.
Do đó sinα + sinβ ≠ 0. Suy ra A sai.
cosα = – cosβ ⇒ cosα + cosβ = 0. Suy ra B đúng.
tanα = – tanβ ⇒ tanα + tanβ = 0. Suy ra C đúng.
cotα = – cotβ ⇒ cotα + cotβ = 0. Suy ra D đúng.
Lời giải
Lời giải
T = sin225° + sin275° + sin2115° + sin2165°
= sin225° + sin275° + sin275° + sin225°
= 2sin225° + 2sin275°
= 2sin225° + 2cos225°
= 2(sin225° + cos225°)
= 2.1 = 2.
Lời giải
Lời giải
Ta có: tanα = – 2 thỏa mãn cosα ≠ 0
P = \[\frac{{{\rm{cos}}\alpha + 3\sin \alpha }}{{\sin \alpha + 3\cos \alpha }} = \frac{{\frac{{{\rm{cos}}\alpha }}{{{\rm{cos}}\alpha }} + 3\frac{{\sin \alpha }}{{{\rm{cos}}\alpha }}}}{{\frac{{\sin \alpha }}{{{\rm{cos}}\alpha }} + 3\frac{{\cos \alpha }}{{{\rm{cos}}\alpha }}}} = \frac{{1 + 3\tan \alpha }}{{\tan \alpha + 3}} = \frac{{1 + 3.\left( { - 2} \right)}}{{ - 2 + 3}} = \frac{{ - 5}}{1} = - 5\].
Vậy với tanα = – 2 thì P = – 5.
Lời giải
Lời giải
Xét tam giác ABC, có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA (định lí cos)
⇔ BC2 = 62 + 82 – 2.6.8.cos100°
⇔ BC2 ≈ 116,7
⇔ BC ≈ 10,8.
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = 2R\)
⇔ \(\frac{{10,8}}{{\sin 100}} = 2R\)
⇔ \(\frac{{10,8}}{{2\sin 100^\circ }} = R\)
⇔ R ≈ 5,5.
Vậy BC ≈ 10,8 và R ≈ 5,5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.