Câu hỏi:
13/07/2024 3,478
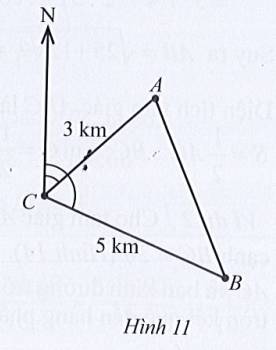
Một cây cao bị nghiêng so với mặt đất một góc 78°. Từ vị trí C cách gốc cây 20m, người ta tiến hành đo đạc và thu được kết quả \(\widehat {ACB} = 50^\circ \)với B là vị trí ngọn cây (Hình 10). Tính khoảng cách từ gốc cây (điểm A) đến ngọn cây (điểm B) (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Xét tam giác ABC, có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc)
⇒ \(\widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right) = 180^\circ - \left( {78^\circ + 50^\circ } \right) = 52^\circ \)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
⇔ \(\frac{{20}}{{\sin 52^\circ }} = \frac{{AB}}{{\sin 50^\circ }}\)
⇔ \(AB = \frac{{20.\sin 50^\circ }}{{\sin 52^\circ }} \approx 19,4\).
Vậy khoảng cách từ gốc cây (điểm A) đến ngọn cây (điểm B) là 19,4 m.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Đáp án đúng là B
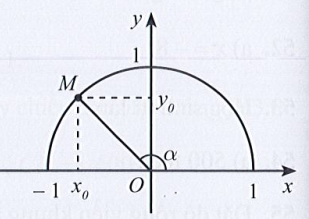
Với 0° < α < 180°, ta có:
– 1 < cosα < 1. Suy ra A sai.
0 < sinα < 1. Suy ra B đúng.
Do đó C và D sai.
Lời giải
Lời giải
Xét tam giác ABC, ta có:
Áp dụng hệ quả của định lí cos, ta được:
\(\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{5^2} + {7^2} - {9^2}}}{{2.5.7}} = - \frac{1}{{10}}\)
⇒ \(\widehat A \approx \)95,7°.
Ta có p = \(\frac{{5 + 7 + 9}}{2} = 10,5\)
Áp dụng công thức herong, diện tích tam giác ABC là:
S =\(\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \sqrt {10,5\left( {10,5 - 9} \right)\left( {10,5 - 7} \right)\left( {10,5 - 5} \right)} \approx 17,4\).
Mặt khác, ta lại có: \(S = \frac{{abc}}{{4R}}\)
⇒ \(R = \frac{{abc}}{{4S}} = \frac{{9.7.5}}{{4.17,4}} \approx 4,5\).
Vậy \(\widehat A \approx \)95,7° và R ≈ 4,5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
15 câu Trắc nghiệm Toán 10 chân trời sáng tạo Không gian mẫu và biến cố có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận